MarchingCubes, SIGGRAPH 1987
Abstract
- output = 연속적인 density값을 갖는 surface의 triangle model
- 알고리즘 큰 흐름 : 3D medical data를 scan-line order에 처리한 후, 선형 보간(linear interpolation)을 이용해서 삼각형의 vertices(꼭짓점)을 구하는 것
Introduction
- mesh extraction하는 것은 medical image에서 굉장히 유용하게 많이 쓰임
- 새로운 3D surface construction 알고리즘인 “Marching Cube”는 연속적인 density surface를 가지는 물체에 대한 vertices를 추출함으로써 고해상도의 메쉬 만듦
- 3D Medical 알고리즘 흐름 :
- Data Acquistion
- MR, CT, SPECT같은 기기로 환자 데이터 얻음
- Image Processing
- 3D data의 전체적인 구조를 파악할 수 있는 기법 사용
- Surface Construction
- 본 논문의 주제, 적절한 알고리즘 사용
- Display
Related Work
기존의 연구
(1) Connected Contour 알고리즘 : surface의 윤곽(contour)에서 시작하여 그것들이 서로 연속적인 삼각형이 되게 연결하는 접근법
-> slice에 하나 이상의 contour가 존재해야하는데 이때 ambiguity(모호성)이 발생하여 정확도 떨어짐
-> 원데이터의 inter-slice의 연결성을 무시함
(2) Cuberille 접근법 : cuberilles(작은 큐브인 voxel형태로 표현하는 구조)로부터 surface 구축하는 접근법
-> 이 구조에서 gradient를 계산했을 때 그 값이 shading(그림자)영역의 지점을 찾는데에 이용되는데, 이게 정확하기가 쉽지 않음
-> thresholding해서 3D space를 블록 단위 voxel처럼 표현하고 surface을 표현
(3) Ray casting
-> 3차원 sensation을 생산하기 위해 motion에 의존함(?)
Marching Cubbe Algorithm (Method)
- 크게 2가지의 주요한 단계로 구성됨
- divide-and-conquer 접근법
- 3D space상의 큐브 하나에서 다음 큐브로 넘어갈 때, surface가 어떻게 교차하는지를 찾는 것이 목표
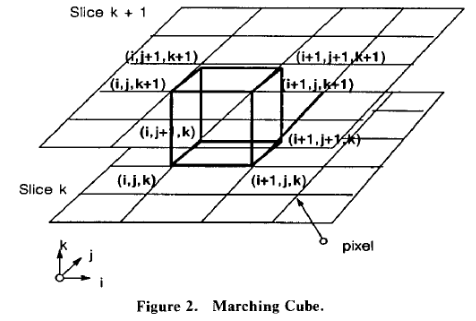
이웃한 8개 픽셀(두 Slice 면의 4개 꼭짓점)로부터 logical한 cube가 Figure-2처럼 위치하게 세팅,
- 큐브의 꼭짓점(vertex) 데이터 값이 우리가 구성하는 surface의 vertex value값을 초과하면 1을 부여
- 마찬가지로 큐브 vertex value가 surface vertex value값보다 아래이면 0을 부여 => surface의 외부에 존재하는 점
대략 이러한 과정으로 교차점들을 통해 surface를 복원하게 된다.
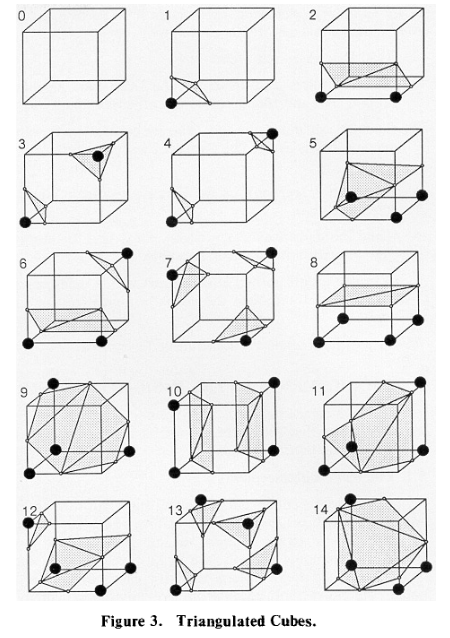
큐브마다 8개의 vertices & 2개의 state(inside, outside)가 존재하기 때문에, 표면이 꼭짓점 1개 당 $2^8$가지 경우의 수로 교차될 수 있다.
- 해당 256가지 경우의 수에 대한 table을 만들 수 있으나 매우 따분하고 에러가 발생하기 쉽기 때문에 , 256가지 경우의 수를 14가지 패턴으로 줄일 수 있는 다음의 두 가지 대칭 속성을 이용함
- 큐브가 reverse로 뒤집혀도, surface value들은 그대로 동일하게 바뀌지 않음
Rotational 대칭
‘’‘(ex) 0번 패턴 : 모든 vertices가 0으로 선택된 케이스(혹은 모두 1) => 삼각형을 생산하지 않게 됨
1번 패턴 : surface가 1개의 vertex를 나머지 7개의 vertices에 대해 분리시킨 상태 => 작은 삼각형 1개
….
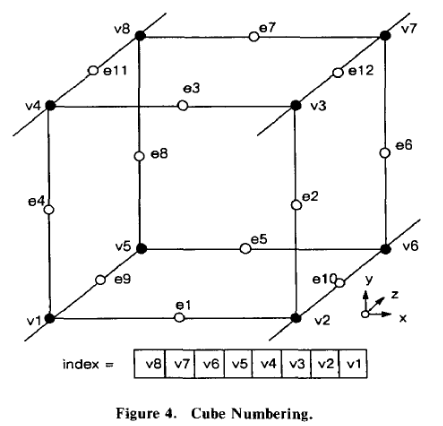
- 이 때, 윗 그림처럼 8개 vertices(v1~v8)와 각 vertex 사이의 bit index 12개(e1~e12)를 numbering하여 edge intersection을 고려한다.
- 그 후 surface와 맞닿는 edge가 어떤 것인지 알았으면, 이 edge들 사이에서 linear interpolation(선형 보간)을 수행한다.
- 마지막 단계로 각 triangle vertex에 대한 unit normal(단위 법선벡터)를 계산한다.
- 이렇게 구한 normal로 Gouraud-shaded image를 렌더링할 때 사용됨, 즉 명암 넣기 단계임
- Details :
- surface 의 normal은, surface의 접선 방향에 대한 gradient vector이다.
direction of gradient vector를 $\vec{g}$로 표기
\[\vec{g}(x,y,z) = \Delta{\vec{f}(x, y,z)}\]
$\Delta{\vec{f}(x,y,z)}$ 를 구하기 위해 3방향에서의 gradient vector를 아래처럼 계산한 후에 선형보간을 하여 surface 복원
\(G_x(i,j,k) = \frac{D(i+1, j, k) - D(i-1, j, k)}{\Delta{x}}\)
\(G_x(i,j,k) = \frac{D(i, j+1, k) - D(i, j-1, k)}{\Delta{x}}\)
\(G_x(i,j,k) = \frac{D(i, j, k+1) - D(i, j, k-1)}{\Delta{x}}\)
In summary, marching cubes creates a surface from a three-dimensional set of data as follows: (논문 표현)
- Read four slices into memory.
- Scan two slices and create a cube from four neighbors on one slice and four neighbors on the next slice.
- Calculate an index for the cube by comparing the eight density values at the cube vertices with the surface con- stant.
- Using the index, look up the list of edges from a precal- culated table.
- Using the densities at each edge vertex, find the surface- edge intersection via linear interpolation.
- Calculate a unit normal at each cube vertex using central differences. Interpolate the normal to each triangle ver- tex.
- Output the triangle vertices and vertex normals