Mip-NeRF 360, CVPR 2022

Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields

• depth distortion loss의 시초
  • 현재 GS기반 Surface Reconstruction 정규화 텀들에 많이 사용함

Abstract

• “unbounded scene” : 학습된 데이터의 방향(direction)과 거리(distance)와 무관하게 모든 ray상에 존재하는 point에 대해 잘 합성된 scene
  • 주로 전경 물체 뿐만아니라 배경까지 있는 scene을 의미함
• NeRF(Neural Radiance Fields)
  • volumentric density 랑 color를 MLP를 통해 합성함
  • MLP : ray상의 작은 3D point들을 이용
• Critical Issues
  1. Parameterization
  2. Efficiency
  3. Ambiguity

Preliminaries : mip-NeRF

• ray : $\mathrm{r}(t) = \mathrm{o} + t\mathrm{d}$ 가 있을 때,
• distance $t$에 의해서 정렬된 벡터가 정의되고 ray가 t에 대한 구간의 집합으로 쪼개진다 $T_i = [t_i, t_{i+1}]$
• 각 구간마다 원뿔대(conical frustum)의 평균과 공분산$(\mu, \Sigma)=\mathrm{r}(T_i)$을 계산함
  • ray의 focal length와 image plane의 픽셀사이즈에 의해서 결정됨

  • featureize 단계(IPE, Integratged positional Encoding)

    \[\gamma(\mu, \Sigma) =\left\{\begin{bmatrix} \sin(2\ell \mu) \exp\left(-2^ {2\ell-1} \operatorname{diag}(\Sigma)\right) \\ \cos(2\ell \mu) \exp\left(-2^ {2\ell-1} \operatorname{diag}(\Sigma)\right) \end{bmatrix} \right\}_{\ell=0}^{L-1}\]
• 위 값들이 MLP의 input으로 들어가고, MLP weight인 $\Theta_{NeRF}$와 같이 들어가서 density $\tau$와 color $\mathrm{c}$를 출력함 :
  • \[\forall T_i \in t, \quad (\tau_i, c_i) = \text{MLP}(\gamma(r(T_i)); \Theta_{\text{NeRF}})\]
• view direction $\mathrm{d}$도 MLP에 같이 들어감

• Volume rendering을 통해 렌더링되는 최종 pixel color $\mathrm{C}(\mathrm{r}, t)$ :

  \[\begin{align} \mathrm{C}(\mathrm{r}, t) = \sum_limits_i w_i c_i \\ w_i = (1-e^{-\tau_i(t_{i+_1} - t_i)})e^{-\sum_{i' < i}\tau_{i'}(t_{i'+1}-t_{i'})} \end{align}\]
• NeRF는 두 개의 서로 다른 MLP (“coarse” MLP와 “fine” MLP)를 사용하는 계층적 샘플링 절차를 사용 :
  • $t^c \sim U[t_n, t_f], \quad t^c = \operatorname{sort}({t^c}) $
  • $t^f \sim hist[t^c, w^c], \quad t^f = \operatorname{sort}({t^f}) $

• final loss (combination of coarse and fine reconstruction loss) :

  \[\sum_{\mathbf{r} \in \mathcal{R}} \frac{1}{10} \mathcal{L}_{\text{recon}} \left( \mathbf{C}(\mathbf{r}, t^c), \mathbf{C}^*(\mathbf{r}) \right) + \mathcal{L}_{\text{recon}} \left( \mathbf{C}(\mathbf{r}, t^f), \mathbf{C}^*(\mathbf{r}) \right)\]

---

1. Scene and Ray Parameterization

1.1. 3D coordinate $x$에 대한 Parameterization

• 기존의 연구들은 unbounded scene에 대해 point를 파라미터화했지만, 본 논문에서는 Gaussian을 재파라미터화하였다
• $f(x)$ : smooth coordinate transformation function 또는 state transition model이라고 정의
• $f$ 에 대한 선형 근사 = $f(x)≈f(μ)+J_f(μ)(x−μ)$
  • where, $J$: $\mu$에서의 f함수에 대한 쟈코비안 행렬
  \[\begin{align} f(μ,Σ)=(f(μ),J_f(μ)ΣJ_f(μ)⊤) \end{align}\]
• Extended Kalman Filter이랑 비슷하게 작동함

  • Contract 함수 : point x를 입력받아 특정 반지름(1,2)를 기준으로 변형하는 연산

    \[\text{contract}(x) = \begin{cases} x, & \text{if } \|x\| \leq 1 \\ \left(2 - \frac{1}{\|x\|} \right) \left(\frac{x}{\|x\|} \right), & \text{if } \|x\| > 1 \end{cases}\]
• 의미
  • x가 1보다 큰 경우(그림에서 주황색 범위인 경우)에는 벡터를 방향은 유지하면서 특정 크기로 축소(수축, contract)
  • 변형된 크기는 $2−1∥x∥2−∥x∥1​$ 로 조정됨 , 벡터를 단위 벡터로 변환한 후 크기를 다시 스케일링하는 방식
  • => 거리가 멀리 떨어져 있을수록 disparity(시점 차) 즉, distance의 역수만큼 비율적으로 분포하게 해줌
  • NDC(normalzed device coordinate)와 같은 motivation
• 본 논문에서는 아래의 식에 따라 유클리드 공간에서 mip-NeRF의 IPE feature encoding($\gamma$) input으로 축소된 공간에서의 contract함수 반환 값($\gamma(\text{contract}(x))$)을 감마 함수에 집어넣는다

2. 구간을 나눌 광선 거리 $t$에 대한 Parameterization :

• 일반적인 NeRF에서는 uniform distribution에서 $t_n$(근거리)과 $t_f$(원거리)사이 구간에서 샘플링한 광선거리 $t^c$를 정렬하여 사용
  • 하지만, Scene parameterization에서 NDC처럼 역할하는 축소된 공간에서의 state transition 과정으로 인해서 실제로는 깊이의 역수(disparity)간격으로 균일하게 샘플들이 배치된다.
  • 이 상황은 카메라 방향이 하나만 존재하는 unbounded scene에는 적합하겠지만, 방향이 다른 모든 뷰에 대한 unbounded scene을 복원하는 데에는 적합하지 않다

• 유클리디안 공간에 있는 ray distance $t$를 “normalized” ray distance $s$로 역매핑해주는 것이 필요 :

  \[s \triangleq \frac{g(t) - g(t_n)}{g(t_f) - g(t_n)}, \quad t \triangleq g^{-1} \left( s \cdot g(t_f) + (1 - s) \cdot g(t_n) \right), \quad (11)\]
  • 여기서 g는 가역(정규화된 값을 출력해주는)함수

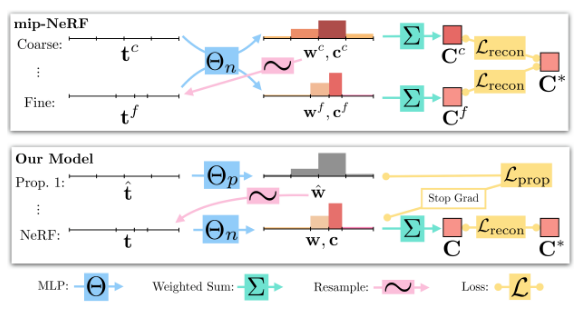
2. Coarse-to-Fine Online Distillation

• Mip-NeRF :
  • MLP에서 “coarse” ray interval $t^c$을 사용하여 한 번 평가하고, 다시 “fine” ray interval $t^f$를 사용하여 평가되며, 두 수준 모두에서 image reconsruction loss를 사용
• Mip-NeRF 360 :
  • 두 가지의 MLP학습(NeRF MLP $\Theta_{NeRF}$ & Proposal MLP $\Theta_{prop}$)
    1. NeRF MLP $\Theta_{NeRF}$ : 기존 Mip-NeRF에서 사용하던 MLP
    2. Proposal MLP $\Theta_{prop}$ : volumetric density만 에측함, color는 예측하지 않음
       • output의 volumetric density가 다시 weight vector $\hat{w}$로 반환됨
       • proposal 가중치 $\hat{w}$는 자체 가중치 벡터 $w$를 예측하는 NeRF MLP에 제공되는 $s$-간격을 샘플링하는 데 사용
       • 입력 이미지를 재현하도록 학습되지 않고 대신 NeRF MLP에 의해 생성된 가중치 $w$를 제한하도록 학습
       • 두 MLP 모두 랜덤하게 초기화되고 공동으로 학습되므로 이 supervision은 NeRF MLP 지식을 proposal MLP에 대한 일종의 “online distillation”로 생각함
  • proposal MLP $(\hat{\mathrm{t}}, \hat{\mathrm{w}})$와 NeRF MLP $(\mathrm{t},\mathrm{w})$의 히스토그램이 일관되도록 장려하는 loss function이 필요
    • 이 때 두 히스토그램 x축 bin길이가 동일할 필요가 없음, 아니 오히려 달라져야 proposal MLP가 잘 학습되었다는 근거임
    • 따라서 bin이 다를 때의 히스토그램 유사성을 평가하는 통계적 방법론 연구들이 상대적으로 부족하기 때문에 꽤 어려운 문제임
      • $\text{bound}(\hat{\mathrm{t}}, \hat{\mathrm{w}}, T) = \sum\limits_{j : T \cap \hat{T}_j neq \emptyset}\hat{w_j} .$
      • 만약 두 히스토그램이 서로 일관(일치)하면, $(\mathrm{t},\mathrm{w})$의 모든 간격 $(T_i, w_i)$에 대해 $w_i \leq \text{bound}((\hat{\mathrm{t}}, \hat{\mathrm{w}}), T_i)$가 모든 구간에 대해 성립해야 함
      • 이 성질 이용해서 $L_{prop}$ 설계 :
      \[\begin{align} \mathcal{L}_{\text{prop}} (\mathbf{t}, \mathbf{w}, \hat{\mathbf{t}}, \hat{\mathbf{w}}) = \sum_i \frac{1}{w_i} \max \left( 0, w_i - \text{bound} (\hat{\mathbf{t}}, \hat{\mathbf{w}}, T_i) \right)^2, \end{align}\]

  

3. Regularization for Interval-Based Models (Depth distortion loss)

• “floater”가 발생하거나 “back-ground collapse”가 발생하는 결함 상황에서 잘 해결할 수 있음

• 정규화된 ray distance $s$와 blending weight $w$간의 step function으로 구성됨

  \[\begin{align} \mathcal{L}_{\text{dist}} (\mathbf{s}, \mathbf{w}) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} w_{\mathbf{s}}(u) w_{\mathbf{s}}(v) |u - v| \, d u \, d v, \end{align}\]
  • where, w_s(u)는 $u$에서 $(s,w)$에 의해 정의된 step function에 대한 보간이다.
  • $ w_s(u)=\sum_i w_i 𝟙[s_i,s_{i+1})(u) $

• 위 적분 식은 정의는 직관적이지만 계산하는 것이 어렵기 때문에, 아래 식으로 rewritten할 수 있음

  \[\begin{align} \mathcal{L}_{\text{dist}} (\mathbf{s}, \mathbf{w}) = \sum_{i,j} w_i w_j \left| \frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2} \right| + \frac{1}{3} \sum_i w_i^2 (s_{i+1} - s_i) \end{align}\]
• 첫 번째 항은 모든 interval에 대한 midpoint사이의 weighted distances 최소화 term, 두 번째 항은 각각의 interval에 대한 weighted size를 최소화하는 텀이다.

느낀점

• 이전에 나온 모델로 Mip-NeRF(ICLR 2021)가 있는데 ray tracing based volume rendering이 아니라, “Cone” tracing한다는 점이 가장 큰 특징인 것만 알고 읽은 상태라 모든 수식이 매끄럽게 이해되진 않았다
• NeRF자체를 제대로 공부해본적이 없었어서 잘 이해가 안되는 게 많긴 하는데 언젠가 공부 급한건 아님