Post

RaDe-GS, arXiv preprint

Posted Updated
By Jiyoung Seo
10 min read
RaDe-GS, arXiv preprint

RaDe-GS: Rasterizing Depth in Gaussian Splatting

Abstract

  • 3DGS의 이산적이고 비구조적인 특성때문에 shape accurac가 떨어지는 문제 있음
  • 최근 관련 연구 중, 2D-GS에서는 shape reconstruction 성능을 올리기 위해, Gaussian primitives들을 이용했지만 이것은 렌더링 퀄리티랑 계산적인 효율성은 감소시키는 효과가 있음
  • 그래서 본 논문에서는 rasterized 접근법을 통해, 3DGS의 depth map과 surface normal map을 렌더링하는 Shape reconstruction 정확성 보장
  • DTU dataset에서 NeuraLangelo와 비교했을 때 CD(Chamfer Distance) error가 좋게 나옴


Introduction

  • multi-view 이미지들로부터 3D Reconstruction하는 태스크에서는 multi-view stereo 알고리즘을 통해 depth map을 얻는 것을 포함한다.
  • 이렇게 얻어진 depth map으로 완전한 triangle mesh를 만드는 모델로 통합되는 것이 가능하다

  • 전통적인 image-based 모델링 접근법은 꽤 정확한 결과로 depth map rendering + mesh recon이 가능하나, 고질적으로 빛나는 표면(shiny surface)이나 reflective한 유리같은 transparent surface에서 특히나 robustness가 떨어지는 한계점이 존재한다.

  • explicit한 3DGS에서 surface 잘 뽑아내는 것은 어려운 문제임
    • 2DGS[Huang et al.2024] : PSNR 수치 줄어듦
    • GOF[Yu et al.2024] : ray-tracing 기반 방법을 통해 광선(light ray)에 따른 Gaussian opacity를 계산하는 방법으로 high-quality surface를 뽑아냄

Contributions

  1. 본 논문에서는 raasterized 기반 방법으로 general Gaussian Splatting에서 정확한 depth map을 얻는 것을 발전시켰다.
  2. standard GS만큼의 computation efficiency를 가진다.
  3. DTU dataset에서 shape reconstruction accuracy를 Chamfer Distance 0.69mm 달성, 5분의 학습시간
    • 이 수치는 implicit한 representation 기반 모델인 NeuraLangelo(0.69mm)와 비슷
    • GS-based 방법론들(sota는 GOF)에서는 당연히 성능 더 좋았음


Methods

  • scene에 splatting된 Gaussian들과 광선에 의한 intersection point를 통한 솔루션을 찾음
💡Key idea💡
> camera center로부터 각각의 Light ray에 의해 Gaussian value가 최대화되는 지점이 intersection point이다
> intersection point들에서 Affine-projection을 시키면 co-planar (동일 평면상에 존재)하다
> 그리고 이 intersection point들을 Image plane에 projection 된 depth로 정의하여 curved surface를 구할 수 있다
> 따라서, planar equation으로 projected depth를 구하는데 이것은 rasterization에 의해 효율적으로 계산될 수 있다.
> final depth map은 투명도(translucency)를 고려하여 투영된 Gaussian들 중에서 중간값 깊이(median depth)로 계산

1. Rasterizing Depth for Gaussian Splats

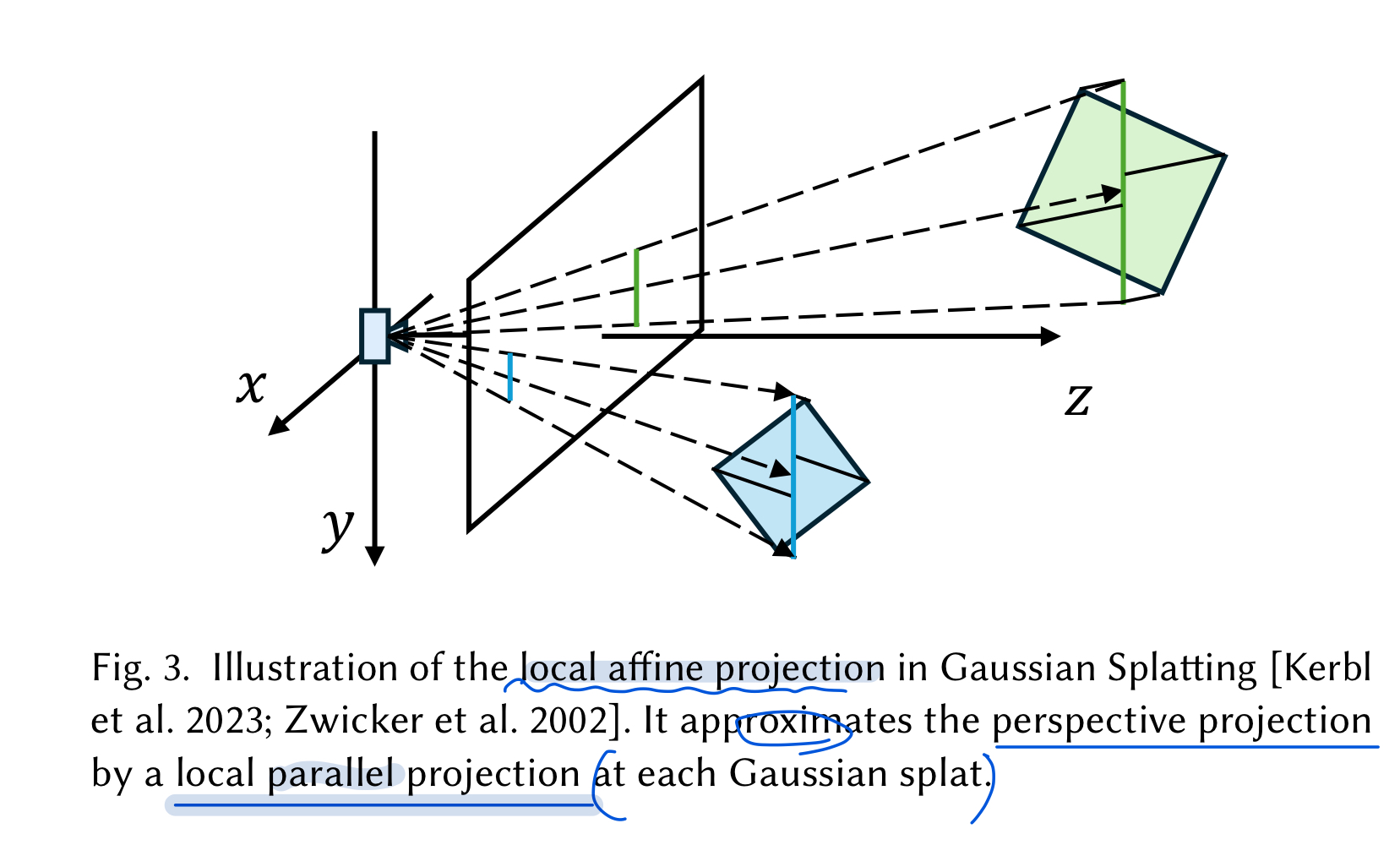
  • Gaussian Splatting에서는 아래 사진처럼 Perspective camera projection을 Affine transformation을 통해 근사시켜서 더 효율적인 rendering가능하다는 것 사전에 알아두고 시작

    figure2

  • standard 3DGS에서는 알파 블렌딩을 위해서 image plane에 projected된 2D Gaussian의 중심점(center)을 depth로 설정한다.
    • shape detail 포착 불가능
  • 그러므로, 본 논문에서는 spatially varying depth를 rasterized method기반 방법으로 계산한다.

1.1. Depth Under Perspective Projection

  • planar equation을 얻는 본격적인 과정 이전에, perspective projection으로 camera coordinate에 대한 기본 concepts부터 먼저 이해해보자.
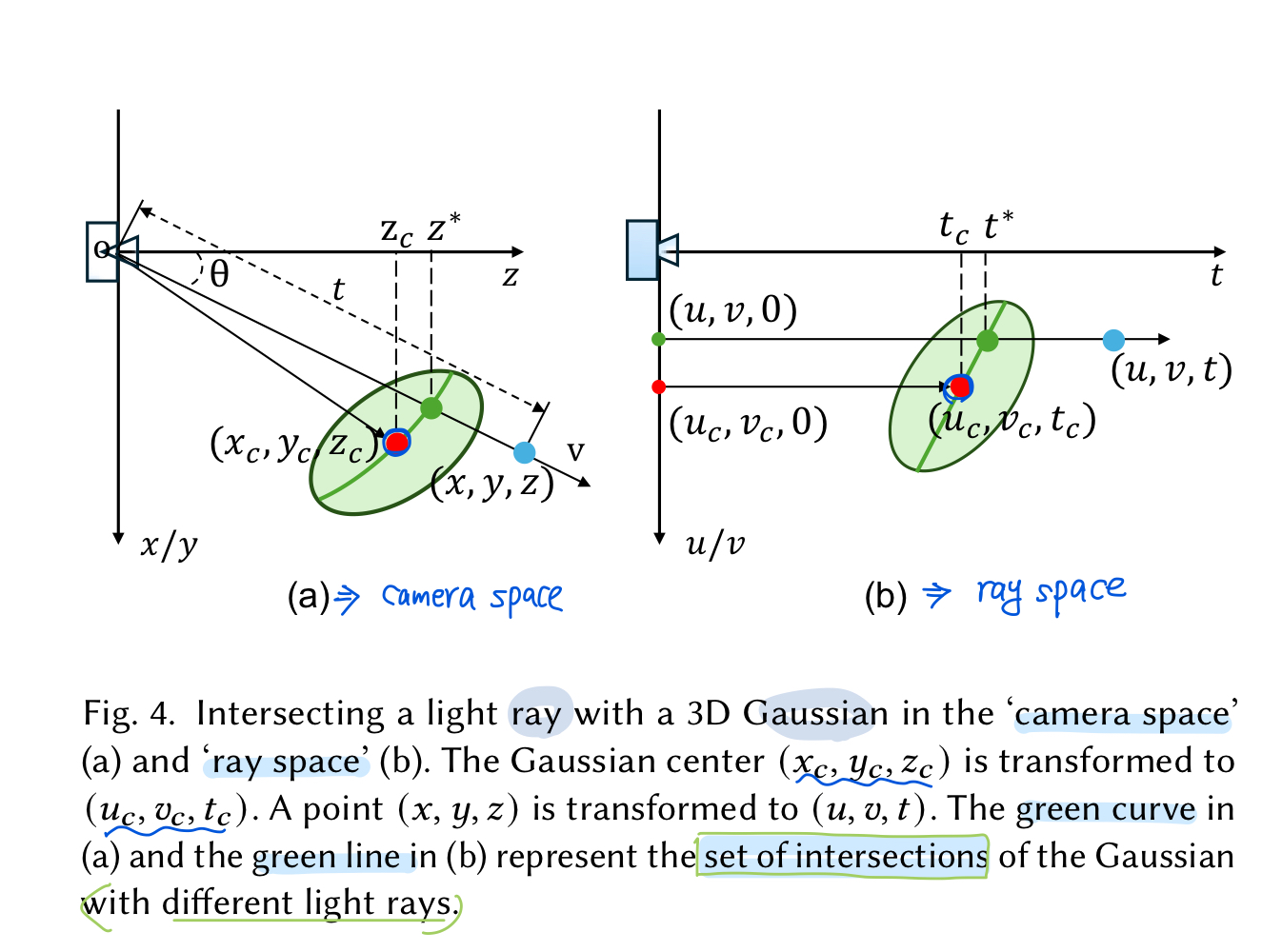
    • Figure 4. img.png

  • 위 그림에서 왼쪽의 (a)에서 보여진 것 처럼, camera center $\mathrm{o}$와 unit direction $\mathrm{v}$가 주어졌을 때,
    ray 상에 $o$로부터 거리 $t$만큼 떨어져 있는 point $\mathrm{x}$는, \(\begin{align} \mathrm{x}= \mathrm{o} + t\mathrm{v} \end{align}\) 으로 구할 수 있다.

  • 이 ray에 존재하는 Gaussian value $\mathrm{G}^1(t)$는, \(\begin{align} \mathrm{G}^1(t)= e^{-(\mathrm{o} + t\mathrm{v}-\mathrm{x}_c)^T\Sigma^{-1}(\mathrm{o} + t\mathrm{v}-\mathrm{x}_c)} \end{align}\) 으로 구할 수 있다.

  • 이 때, Gaussian value는 1-D function이고, 이 값이 최대화되는 지점이 3D Gaussian과 ray가 만나는 “intersection point” 라고 정의한다.

  • 그 후 distance $t^*$ : intersection point와 camera center간의 거리는 위의 Gaussian value가 최대화되는 t를 찾으면 되고 구한 식은 아래처럼 됨

    \[\begin{align} t^* = \frac{\mathrm{v}^T\Sigma^{-1}(\mathrm{x}_c - \mathrm{o})}{\mathrm{v}^T\Sigma^{-1}\mathrm{v}} \end{align}\]

    (유도 과정) :

    figure

  • 이렇게 유도된 distance $t^*$이 의미하는 바는, 3D Gaussian들과 광선들 집합간의 intersection들이 “curved surface”(연두색 곡선) 를 나타낸다고 해석할 수 있음
    • different pixels have different depth values of $t^*$ and different viewing direction $\mathrm{v}$.


1.2. Depth Under Local Affine Projection

  • 이제 가우시안말고, 픽셀의 depth를 “local affine projection”으로 구해보자.

  • 위의 Figure4.(b)상황 => “ray space” 좌표계

    [1.2.1. Transformation from Camera to Ray space]
    • (a) 의 파란 점 $\mathrm{x} = (x, y, z)^T$ 가 (b)의 파란 점 $\mathrm{u} = (u,v,t)$ 로 변환
    • $(u,v,t)$에서 $(u,v)$는 image plane coordinate(이미지 평면에서의 좌표계)이고, $(t)$는 point와 $uv-plane$사이의 거리를 나타낸다
    • 즉, $t=\sqrt{x^2+y^2+z^2}$

    • ray space에서 light direction $\mathrm{v}$ 는 단위고유벡터 $(0,0,1)^T$임

    • 가우시안들도 ray space로 변환되어야 하는데, 변환된 Gaussian Function은 아래와 같다

      \[\begin{align} \mathrm{G}'(\mathrm{u}) = e^{-(\mathrm{u}-\mathrm{u_c})^T\Sigma^{'-1}(\mathrm{u}-\mathrm{u_c})} \end{align}\]

      Gaussian center $\mathrm{u_c}=(u_c, v_c, t_c)^T$로, (b)그림에서 빨간 점


    [1.2.2. Intersection in Ray Space]

    기본 과정은 perpective projection때와 같음

    1) ray space 상에 존재하는 point $\mathrm{u}$  :

    \[\begin{align} \mathrm{u} = \mathrm{u_o} + t\mathrm{v'} \end{align}\]

    where , $\mathrm{u_o} = (u,v,0)^T \quad and \quad \mathrm{v’} = (0,0,1)^T $

    2) 1D Gaussian function $\mathrm{G^{‘1}}(t)$ :

    \[\begin{align} \mathrm{G^{'1}}(t)= e^{-(\mathrm{u_o} + t\mathrm{v'}-\mathrm{u_c})^T\Sigma^{'-1}(\mathrm{u_o} + t\mathrm{v'}-\mathrm{u_c})} \end{align}\]

    3) maximum point가 위치한 distance $t^*$ :

    \[\begin{align} t^* = \frac{\mathrm{v'}^T\Sigma^{'-1}(\mathrm{u}_c - \mathrm{u_o})}{\mathrm{v'}^T\Sigma^{'-1}\mathrm{v'}} \end{align}\]

    간단하게 표현하기 위해서 $(\mathrm{u}_c - \mathrm{u_o})$ 벡터 빼고 나머지 항들을 $\hat{q}$로 정의하여 간단하게 아래처럼 표현 :

    \[\begin{align} t^* = \hat{q}(\mathrm{u}_c - \mathrm{u_o}) \end{align}\]


    [1.2.3. Depth of Intersection]

    1) $t$는 3D point $x$와 camera center $o$사이의 거리이므로 x에 대한 깊이는, 간단하게 삼각비 성질을 이용해서 (a)그림의 $z^*$을 아래처럼 구할 수 있다:

    \[\begin{align} d = cos\theta t^* \end{align}\]

    2) (b), affine projection인 상황에 대입해서 depth구하면,

    \[\begin{align} d = cos\theta_c t^* = \frac{x_c}{t_c}t^* = \frac{x_c}{t_c}\hat{q}(\mathrm{u}_c - \mathrm{u_o}) = \hat{p}(\mathrm{u}_c - \mathrm{u_o}) \end{align}\]

    여기서 $\hat{p} = \frac{z_c}{t_c}\hat{q}$로 정의

    3) 이어서 위의 식을 아래처럼 나타낼 수 있는데,

    \[\begin{align} d = \hat{p}(\mathrm{u}_c - \mathrm{u_o}) = \hat{p}\begin{pmatrix} u_c - u \\ v_c-v \\ t_c \end{pmatrix} = \hat{p}\begin{pmatrix} 0 \\ 0 \\ t_c \end{pmatrix} + \hat{p}\begin{pmatrix} \Delta{u} \\ \Delta{v} \\ 0 \end{pmatrix}. \end{align}\]

    4) 위의 최종 분해된 식 중, 첫 번째 항 $\begin{pmatrix} 0 \ 0 \ t_c \end{pmatrix}$에 대한 성질 :

    \[\begin{align} \hat{p} \begin{pmatrix} 0 \\ 0 \\ t_c \end{pmatrix} &= \frac{z_c}{t_c} \hat{q} \begin{pmatrix} 0 \\ 0 \\ t_c \end{pmatrix} \\ &= \frac{z_c}{t_c} \frac{\mathrm{v^{'T}}\Sigma^{'-1}}{\mathrm{v^{'T}}\Sigma^{'-1}\mathrm{v'}} \begin{pmatrix} 0 \\ 0 \\ t_c \end{pmatrix} \\ &= \frac{z_c}{t_c} \frac{\mathrm{v^{'T}}\Sigma^{'-1}}{\mathrm{v^{'T}}\Sigma^{'-1}\mathrm{v'}} (t_c\mathrm{v'}) \\ &= \frac{z_c}{t_c} \frac{\mathrm{v^{'T}}\Sigma^{'-1}\mathrm{v'}}{\mathrm{v^{'T}}\Sigma^{'-1}\mathrm{v'}} (t_c) \\ &= z_c . \end{align}\]


    5) 두 번째 항의 $\hat{p}$ 는 $p$ 로 근사됨

    • 따라서, 최종적으로 depth를 구하는 rasterized method수식으로 유도된다.
    • Recall. $d = z_c + p(\begin{pmatrix} \Delta{u} \ \Delta{v} \end{pmatrix})^T$


2. Rasterizing Normal for Gaussian Splats



느낀점

  • 이 분야에서는 살짝 뭐 바꿨더니 소타다 이런건 절대 안먹히겠다
  • 완전히까진 아니여도 적당히 창의적으로 메소드를 짜야되겠구나라는 생각이 들었다. 이런 면이 재밌지만서도 다소 막막하긴 하다
  • Affine aprroximation projection기반으로 spatial varying depth 구하는 방법이 창의적이다
  • 2DGS에서 쓴 loss 가져다 쓴 건 아쉬운데 이거까지 새로 짰으면 걍 씨그라프 오랄 찍었을 것 같다
  • 이건 어셉 왜 안되지
    • GOF(SIGGRAPH Asia 2024)가 작년 9월에 나와서 sota인 것 같다. 이어서 이거 읽기
Paper Review
Surface reconstruction stereo vision Graphics
This post is licensed under CC BY 4.0 by the author.