SuGaR, CVPR 2024

Abstract

• precise and extremely fast mesh extraction from 3DGS representation
• state-of-the-art method on SDFs, while providing a better rendering quality

Contributions

1. Regularization term
   • Gaussian Splatting 최적화 중의 loss term에 추가시켜서 3D Gaussian들이 표면에 잘 정렬되게 하는 역할
   • 3D Gaussian의 surface geometry(density & SDF)를 이용함
2. Refinement strategy
   • mesh에 있는 gaussian들 삼각형으로 묶어주면서 refinement함

Introduction

• mesh extraction task는 3DGS representation의 explicit한 특성 때문에 더 어려움
• 3DGS가 잘 최적화되었으면, 가우시안들이 평평하고 표면에 잘 분포되어있다는 가정을 얻을 수 있음
  • 이때 gaussian density와 관련된 geometry를 이용해서 Loss term에 추가하면서 gaussian으로부터 mesh추출이 더 쉬워지게 만듦
  • volumne density 사용?
• Marching Cube 알고리즘 대신 Poisson Reconstruction 알고리즘 사용해서 point cloud로부터 mesh extraction을 했다

Method

1. Aligning the Gaussians with the Surface (=Regularization)

• 목표 : 3DGS가 잘 최적화되어있다는 가정 하에, Gaussian의 SDF(Signed Distance Function)를 이끌어내는 것

• optimized된 가우시안으로부터 예측된 SDF와 실제의 SDF간의 차이를 최소화함으로써 가우시안들이 평평하게 surface align된 특성을 갖을 수 있도록 encourage

• 최적화된 Gaussian Splatting Scene이 주어져있는 상황에서 시작

  Gaussian의 density function $d(p)$ :

  \[d(p) = \sum_g \alpha_g exp(-\frac{1}{2}(p-\mu_g)^T\sigma_g^{-1}(p-\mu_g))\]

< Property 1 >

\[g^* = \arg\min_g(p-\mu_g)^T\sigma_g^{-1}(p-\mu_g)\]

해석 = g*말고 나머지 가우시안들, g들에 대한 밀도가 최소가 되게 하면 된다.

⇒ 이 성질을 만족하면, 가우시안들이 scene에서 잘 spread되어있다, 즉 scene에 가우시안들이 잘 퍼져있다는 가정을 만족

< Property 2 >

\[(p-\mu_g)^T\Sigma_g^{-1}(p-\mu_g) \approx \frac{1}{s_g^2}<p-\mu_g, n_g>\]

[notation]

• $s_g$: 가장 짧은 scaling factor
• $n_g :$ scaling factor에 대응되는 축에 대한 방향, normal(법선 벡터)처럼 생각해도 됨

⇒ 결과적으로 surface-align한 density function $\overline{d}(p)$

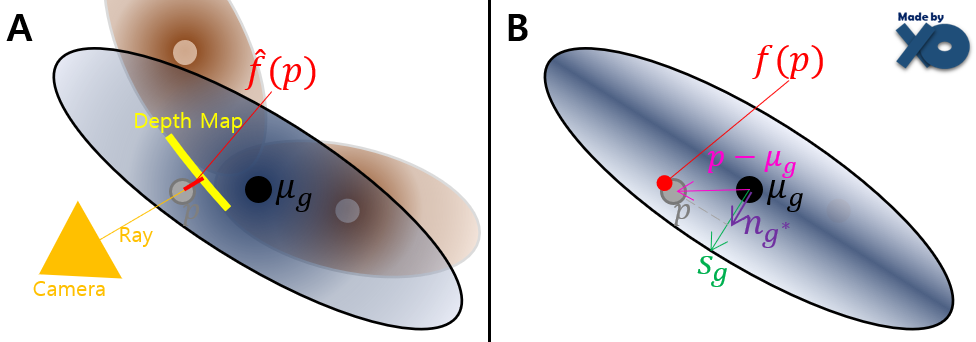
\[\overline{d}(p) = exp(-\frac{1}{2s_{g^*}^2} <p-\mu_{g^*}, n_{g^*}>^2)\]

• A : d(p) 밀도함수를 따르는 가우시안,
• B : $\overline{d}(p)$ 밀도함수를 따르는 가우시안

< Optimize Term >

1. $|d(p) - \overline{d}(p)|$: 위의 density volume을 이용한 optimization term 을 3DGS loss에 추가
   • 밀도를 이용하는 지금 optimize term 일단 좋긴 좋은데,,,density말고 SDF(Signed Distance Function) 활용하는 것도 추가시키면 surface-align Gaussian을 얻는 것에 더 좋다고 함 - 평평한 가우시안이 주어졌을 때, 즉 Gaussian $g$의 scaling factor들이 $s_g$ = 0 인 상황에서, point $p$와 true surface와의 거리 : $|<p-\mu_{g’}, n_{g’}>|$

\[SDF : \overline{f}(p) = \pm s_{g^*}\sqrt{-2log(\overline{d}(p))}\] \[ideal-SDF : {f}(p) = \pm s_{g^*}\sqrt{-2log({d}(p))}\]

1. $|\overline{f}(p)-f(p)|$ : 위의 SDF를 이용한 optimization term을 통해 표면에 더 잘 정렬된 가우시안들을 얻을 수 있었다.

• Regularization term $R$ :

\[R = \frac{1}{|P|} \sum_{p \in P} |\overline{f}(p) - f(p)|\]

• SDF의 normal(법선 벡터)에 대한 regularization term도 있음

  \[R_{Norm} = \frac{1}{|P|} \sum_{p\in P} || \frac{\nabla f(p)}{|| \nabla f(p) ||^2} - n_{g^*} ||_2^2\]

---

2. Efficient Mesh Extraction (=Poisson Reconstruction)

• 최적화된 3DGS scene에서 계산된 가우시안들의 density로부터 3D points를 일정 level set에 대하여 샘플링함 => point clouds 구함

  • 이 때, level set은 level parameter인 $\lambda$에 의해 결정됨

    

• 샘플링된 Points 기반으로 Poisson reconstruction 수행하여 mesh 추출

  참고. Poisson Reconstruction 정리 글

---

3. Binding New Gaussians to the Mesh (=Refinement)

• Barycentric 좌표계 : 삼각형 또는 다면체 내부의 점을 해당 도형의 꼭짓점에 대한 가중치로 표현하는 좌표계
  • (ex) 삼각형의 경우:

    • 삼각형의 꼭짓점을 A, B, C라 할 때, 내부의 임의의 점 P는 다음과 같이 표현됩니다:

      $P = \alpha A + \beta B + \gamma C$

    • 여기서 α,β,γ는 가중치로, 아래 조건을 만족합니다:

      $\alpha + \beta + \gamma = 1$

• 논문 표현 :

  Also, the Gaussians have only 2 learnable scaling factors instead of 3 and only 1 learnable 2D rotation encoded with a complex number rather than a quaternion, to keep the Gaussians flat and aligned with the mesh triangles.

• quaternion이란: 3D 회전을 표현하기 위해 사용되는 수학적 구조로, 복소수의 확장된 형태

  $q=w+xi+yj+zk$

---

Experiment

• single GPU Nvidia Tesla V100 SXM2 32 Go

느낀점

• 3DGS에서 거의 최초로 mesh reconstruction태스크를 수행해서 성능이 좋게 나왔다는 것이 의의
• 요즘 모델들의 거의 baseline 시초급(?)으로 봐도 무방하다
• 포아송 재건방법이 아직 뭔지 잘 모르겠다. marching cube공부할 때 같이 공부
• 어렵긴 한데 재밌다.