Graphics-Ch10. Surface shading

1. Diffuse Shading

• Lambertian objects
  • paper, wood, dry, unpolished stone같은 모든 면에서 빛이 난반사(diffuse)되는 불투명한 표면의 물체
• perspective transformation이후의 warped coordinate에서 생각하는 것이 아닌, world coordinate에서의 shading 적용을 고려함

1.1. Lambertian Shading Model

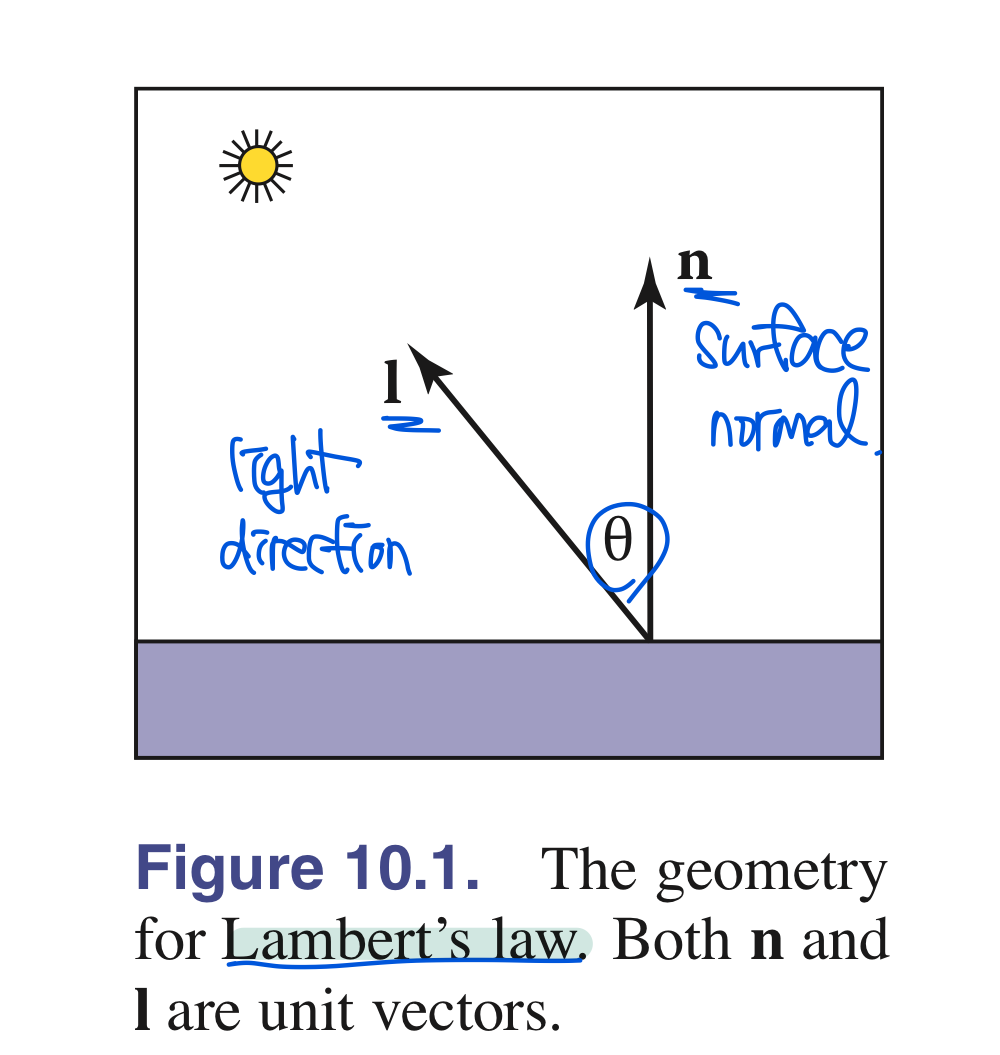
• “Lambert’s cosine law” :
  

  \[\begin{align} c &\propto cos \theta . \\ c &\propto \mathrm{n} \cdot \mathrm{l}, \end{align}\]
  • $c$ : surface color
  • $\mathrm{n}$ : surface normal
  • vector $\mathrm{l}$ : light direction (물체가 놓여진 표면의 위치에 영향을 받지 않는다는 중요한 성질 있음)
• 광원의 세기(intensity)와 표면의 반사도(reflectance)에 따라 표면은 더 밝아지거나 어두워질 수 있음
  • $c_r$ : diffuse reflectance (diffuse object 표면에서 흡수대비 반사되는 빛의 비율)
  \[\begin{align} c \propto c_r \mathrm{n} \cdot \mathrm{l}. \end{align}\]
  • $c_l$ : RGB intensity term (in the range [0,1])
  \[\begin{align} c = c_r c_l \mathrm{n} \cdot \mathrm{l}. \end{align}\]

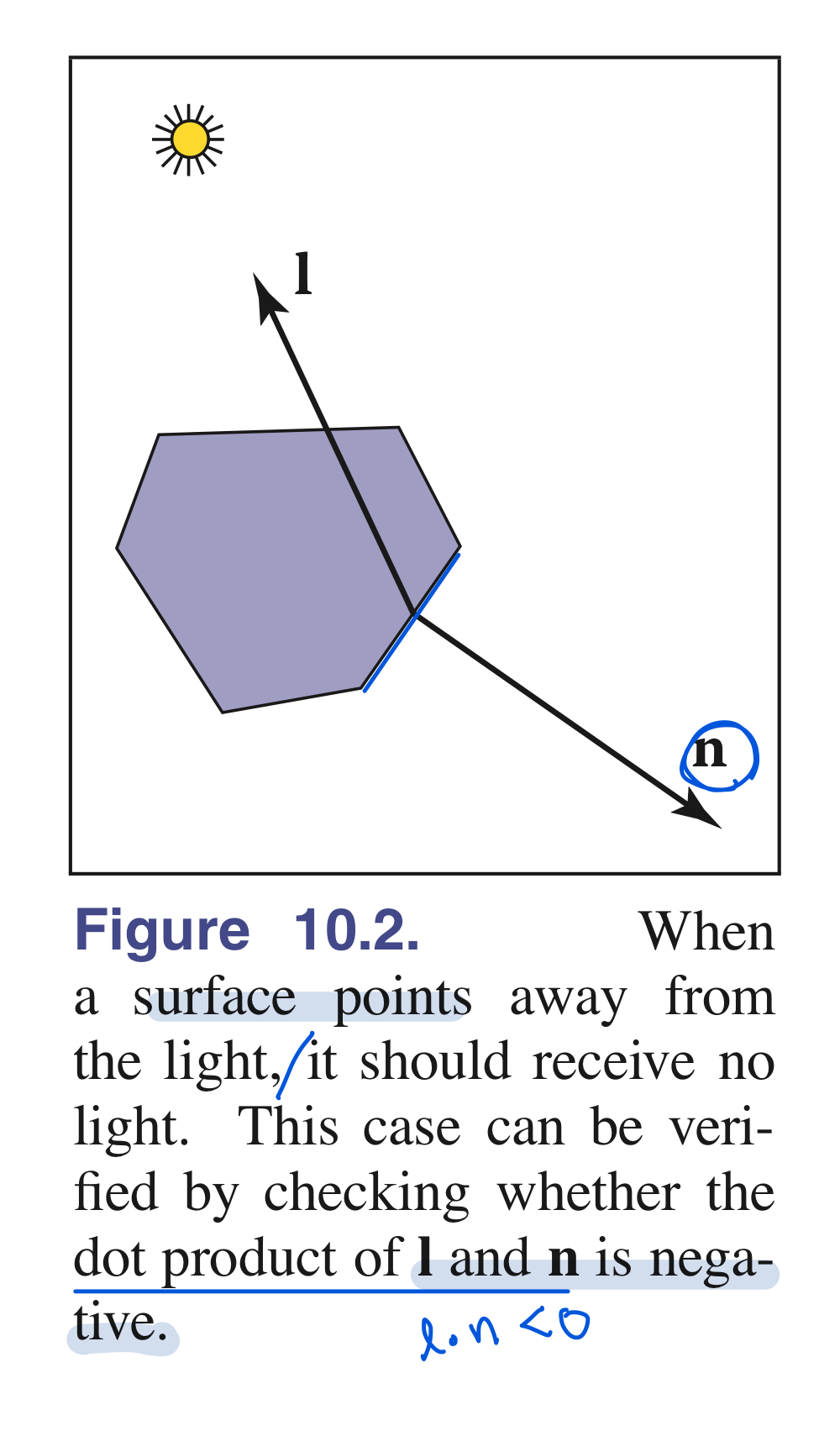
• 이 때, $n \cdot l$은 만약 surface normal이 light direction과 정반대 즉, 두 벡터 사이 각도 $\theta$가 180도 이상인 경우는 dot product값이 음수가 나오는 상황이므로, 내적연산을 “max” function으로 대체할 수 있음 :

  \[\begin{align} c = c_r c_l max(0, \mathrm{n} \cdot \mathrm{l}). \end{align}\]

1.2. Ambient Shading

• 실제 환경에서 모든 방향의 광원을 고려하다보면 diffuse shading만으로 완벽하게 실제 조명을 구현하기에 충분하지 않다는 문제

• 상수항(ambient term)을 더해줌

  \[\begin{align} c = c_r (c_a + c_l max(0, \mathrm{n} \cdot \mathrm{l})). \end{align}\]

2. Phong Shading

• 모든 표면이 lambertian suface일 수는 없다, highlight되는 부분이 포함된 matte surface인 경우의 light shading model

2.1. Phong Lighting model

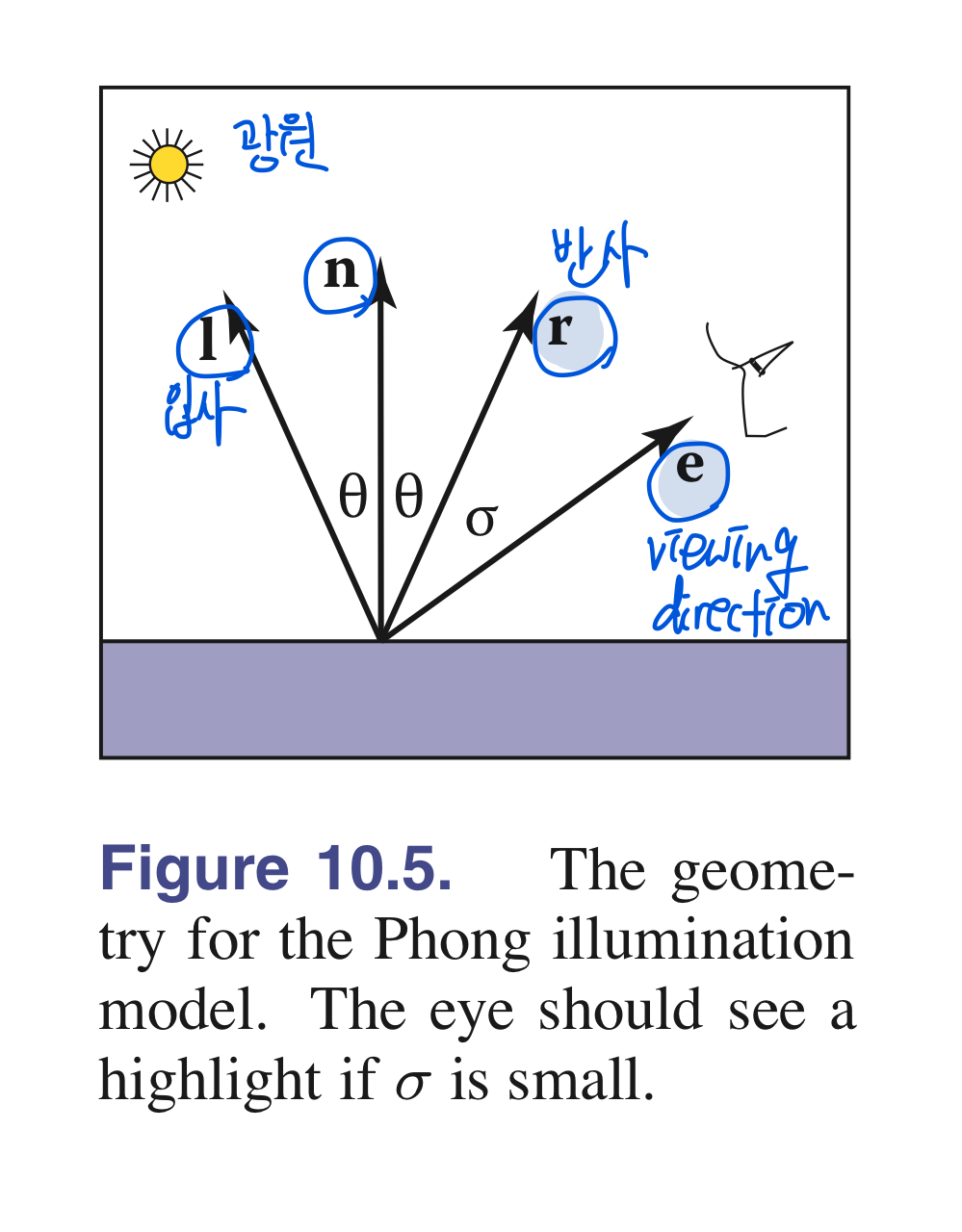
• $\mathrm{r}$ : natural direction of reflection(입사되는 빛과 같은 각도 $\theta로 반사되는 방향의 벡터)

• unit vector $\mathrm{e}$ (viewing direction)를 추가시킴

  \[\begin{align} c &= c_l (\mathrm{e} \cdot \mathrm{r}) . \\ c &= c_l max(0, \mathrm{e} \cdot \mathrm{r}) ^p \end{align}\]
  • $p$ : Phong exponent
    • 양의 실수임
    • 이 값에 따라 highlight되는 영역의 크기와 세기가 아래 그림의 figure 10.6처럼 변화됨

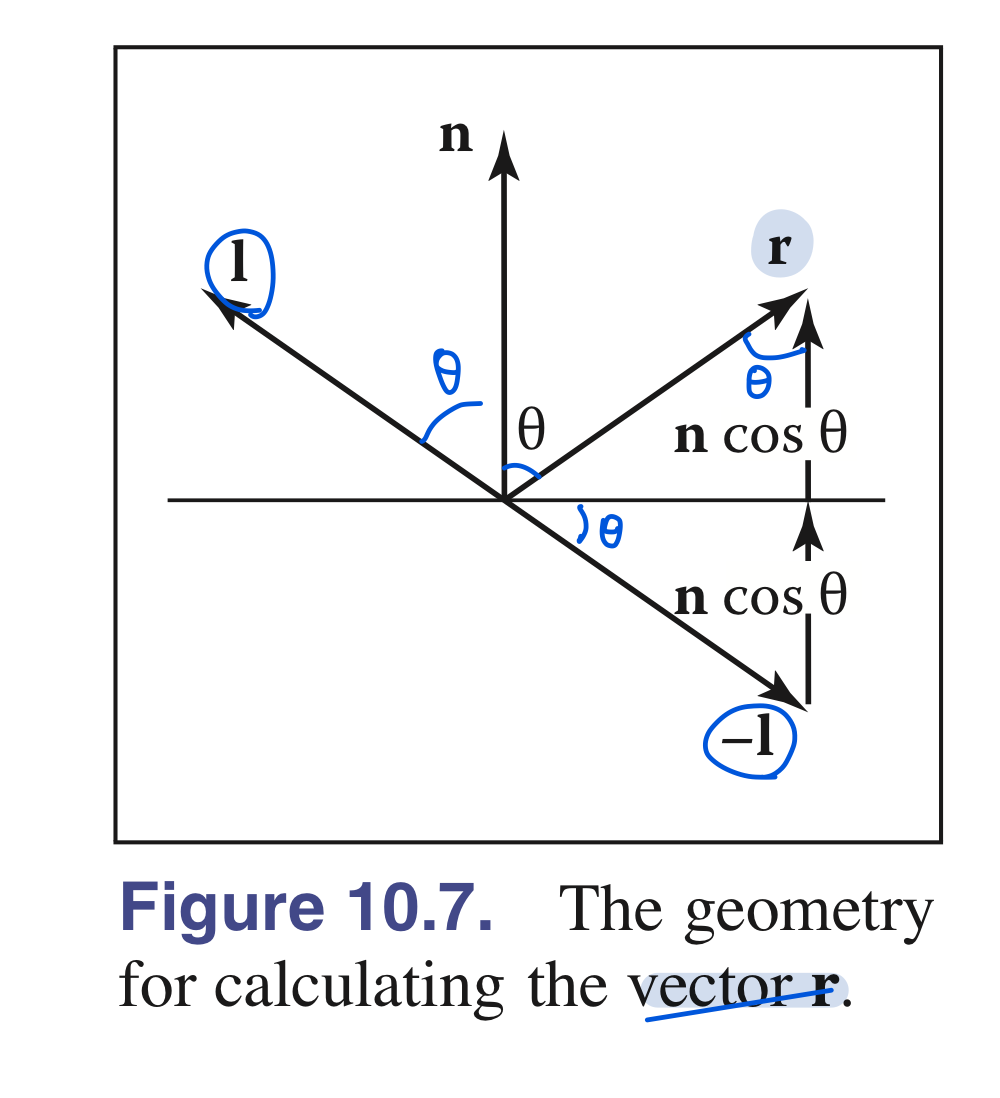
• 아래 그림처럼 벡터 $\mathrm{r}$은 입사 방향 $\mathrm{l}$과 n을 기준으로 각도 $\theta$만큼 대칭되게 존재한다는 성질로 아래 수식으로 r 계산 가능 :

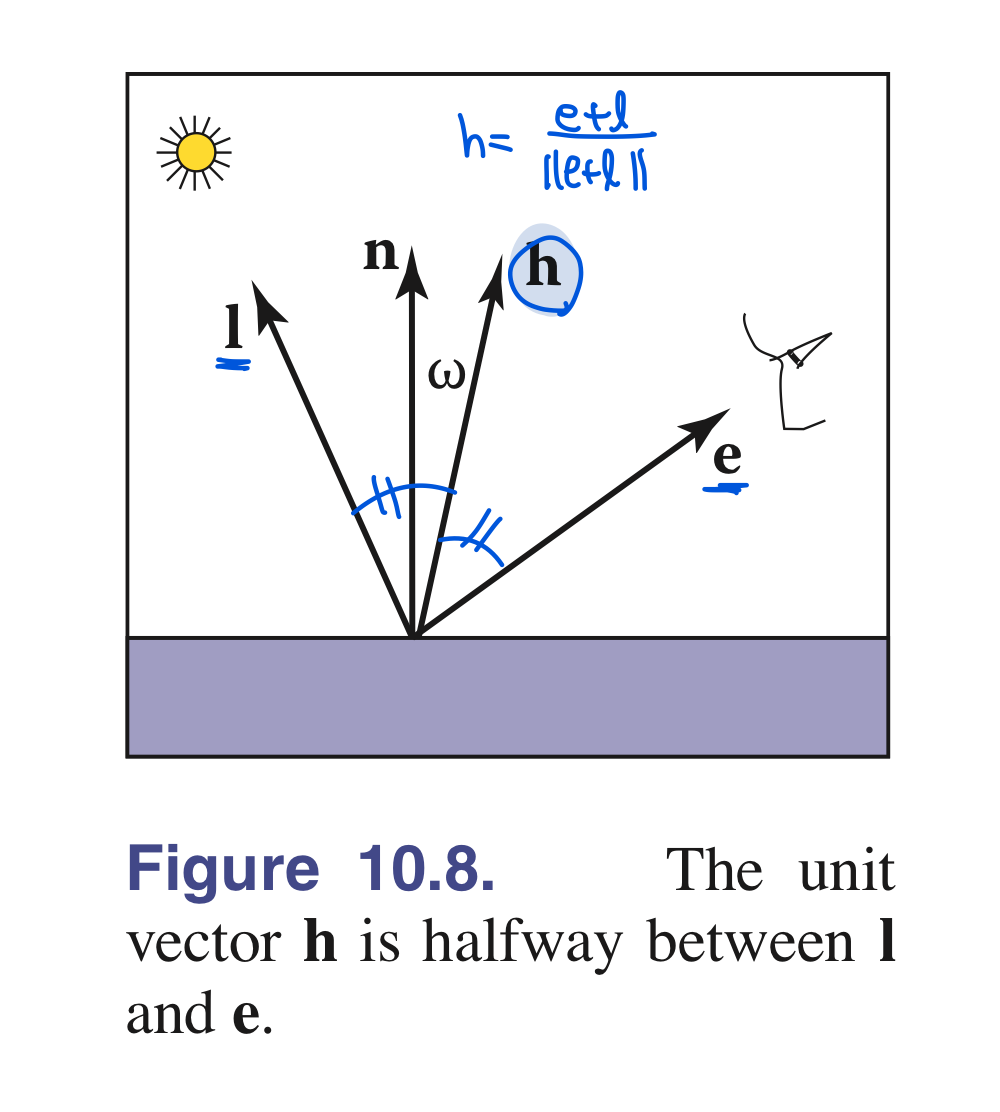
  \[\begin{align} \mathrm{r} = -\mathrm{l} + 2(\mathrm{l} \cdot \mathrm{n})\mathrm{n}, \end{align}\]
• $\mathrm{r}$대신 휴리스틱하게 $\mathrm{l}$과 $\mathrm{e}$의 가운데 존재하는 halfway vector $\mathrm{h}$를 이용하여 highlight 영역 light modeling 가능함
  • n과 h의 내적은 항상 양수라는 장점 있음
  • 단점은 h 계산을 위해서는 루트 연산과 나눗셈이 필요함
• $\mathrm{h}$가 $\mathrm{n}$ 과 가까울수록 highlight가 커진다고 해석 가능

• 이때, h와 n 사이의 각도는 $\theta$보다 작아질 수밖에 없어서 디테일이 살짝 달라질수는 있다

  \[\begin{align} &c = c_l (\mathrm{h} \cdot \mathrm{n})^p , \\ &where, \quad \mathrm{h} = \frac{\mathrm{e} + \mathrm{l}}{|| \mathrm{e} + \mathrm{l} ||} \end{align}\]

• 최종 Phong illumination model :
  • ambient light term, diffse(lambertian) term, highlight term이 순서대로 더해진 전체 shading model 수식
  \[\begin{align} c = c_r(c_a + c_l max(0, \mathrm{n} \cdot \mathrm{l})) + c_l c_p (\mathrm{h} \cdot \mathrm{n})^p \end{align}\]
  • $c_p$ : RGB color, which allows us to change highlight colors