Graphics-Ch3. Raster Images

Chapter 3. Raster Images

서론

• Raster image : 2D 행렬 형태로 픽셀에 대한 RGB color값을 표현한 이미지
  • RGB 색상은 3차원 벡터 형태
• 디지털 카메라는 image sensor를 포함하고 있는데, 이것은 빛이 들어오는 정도(intensity)와 color를 구성하고 있음
• 하지만 우리가 이러한 2D array자체로 이미지를 보지는 않음,
  • 이미지 픽셀과 디스플레이 픽셀간의 매칭(direct link)이 필요하고 이를 Rasterizer가 처리함
• Vector Image : 픽셀에 대한 행렬형태로 나타내는 것이 아니라, shape이랑 line, curves로 경계지어진 color 영역에 대한 이미지 표현
  • resolution independent하다는 점과, 고해상도로 displayed된다는 점이 장점이지만 display되기 이전에 rasterized되어야 한다는 점이 단점이다.
    
• 이번 챕터에서는 Raster Image를 다루며, 빛의 세기(light iintensity)와 연관된 pixel value를 어떻게 결정하는지에 대한 자세한 내용은 나중 챕터에서 다룰 예정이니 일단 기억해두기.
  
  

1. Raster Devices

• 장치를 Raster한다는 것은 무슨 의미일까
• input output을 간단한 조직도로 나타낸 사진은 아래와 같다.

1.1. Displays

• pixel value에 대한 고정된 2D array 기반으로 디스플레이되어지는데, 방식이 두 가지로 분류 가능함
  

1) Emissive(방출하는) Display : 픽셀들이 direct하게 조절가능한 light를 방출하는 방식

• 픽셀 자체가 광원이 됨
• LED(Light-Emitting Diode)가 대표적인 예시

2) Transmissive(투과하는) Display : 빛을 방출하진 않고, 대신에 투과할 수 있는 만큼의 빛을 픽셀이 갖고 있는 방식

• transmissive display는 픽셀 행렬 뒤에 backlight가 필요함, 어느정도 illuminate(밝게 하다)될 만큼의 광원이 필요하기 때문
• LCD(Light-Crystal Display)가 대표적인 예시
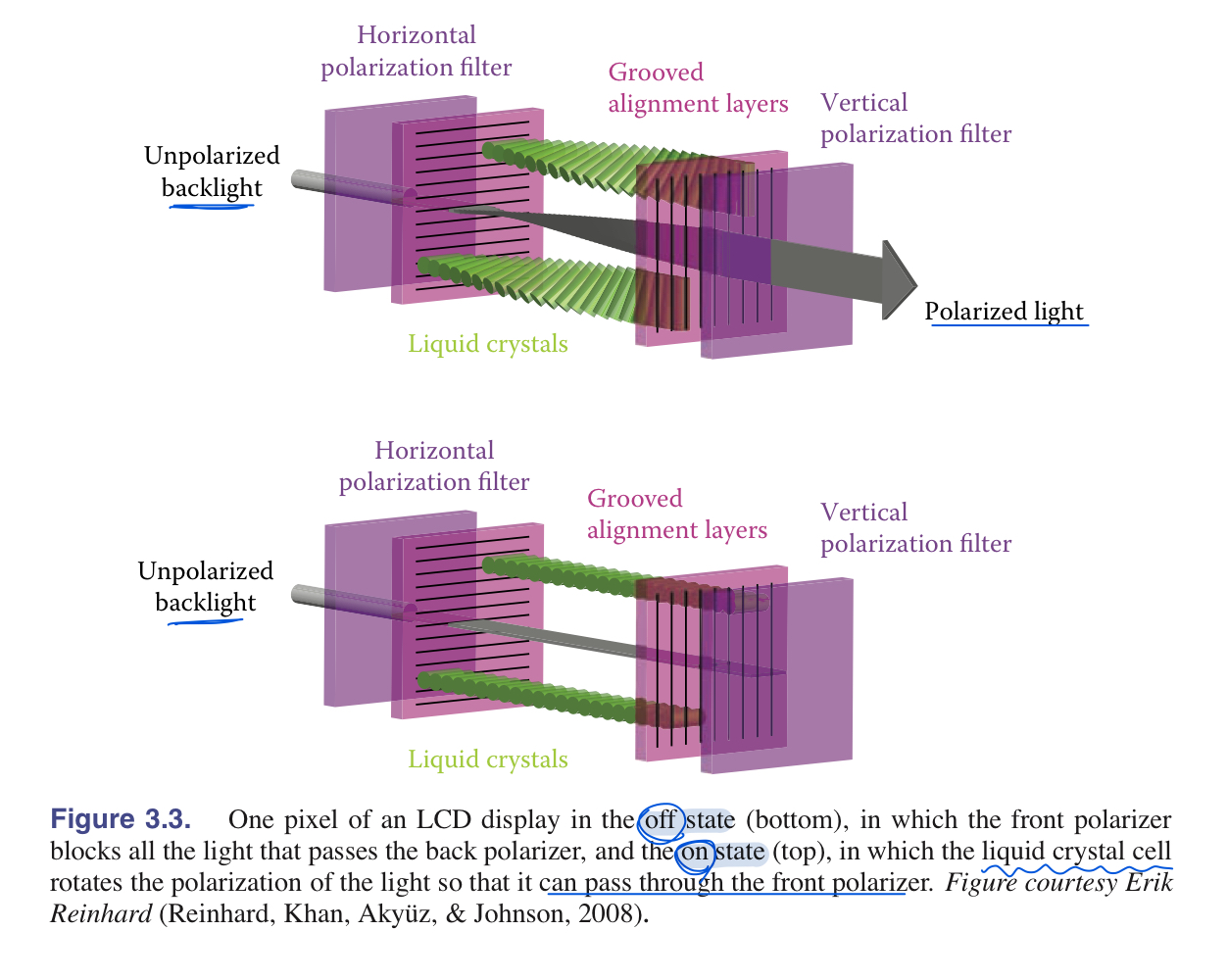
• on-state(위, 전압 들어온 상태)가 되면 liquid crystal cell이 회전하면서 polarized light이 front plarizer를 투과할 수 있게 해주는 원리
  
  

2. Images, Pixels, and Geometry

• Raster Image는 이미지 픽셀별로 RGB 색상에 대한 값을 2차원 행렬 형태로 나타내는 것을 알고 있다.
• 이미지를 측정하거나 reproduce할 때, light energy에 대해 다음의 2차원 분포를 알아야 한다 ;

  1. light emitted from the monitor as a function of a position on the face of the display
     = 디스플레이 표면에서 방출되는 빛

  2. light falling on a camera’s image sensor as a function of a position across the sensor’s plane
     = 카메라의 이미지 센서로 들어가는 빛
     

  • Reflectance(반사율) 또는 흡수되는 빛 대비 반사되는 빛의 비율(fraction)
    = function of position on a piece of paper

• We can abstract an “image” as a function $I(x,y)$:
  \(I(x,y) : R -> V\)
  

  • grayscale 이미지인 경우에는 $V$가 양수구역이고, ideal한 color image인 경우에 $V$는 3차원 실수 공간영역이다.

• continuous(연속적인)값으로 어떻게 Raster image가 표현되는 것인가.
  • Point sampling과 관련있다, 자세한 것은 chapter 9의 신호처리단원에서 다룬다고 한다
  • 이미지의 색상에 대한 Local average를 pixel value정함
  • pixel value인 x를 구한다는 말은 즉, “the value of the image in the vincinity(주변) of the grid point is x”를 구한다는 것과 같은 말이다. (당연한거아님?)
    
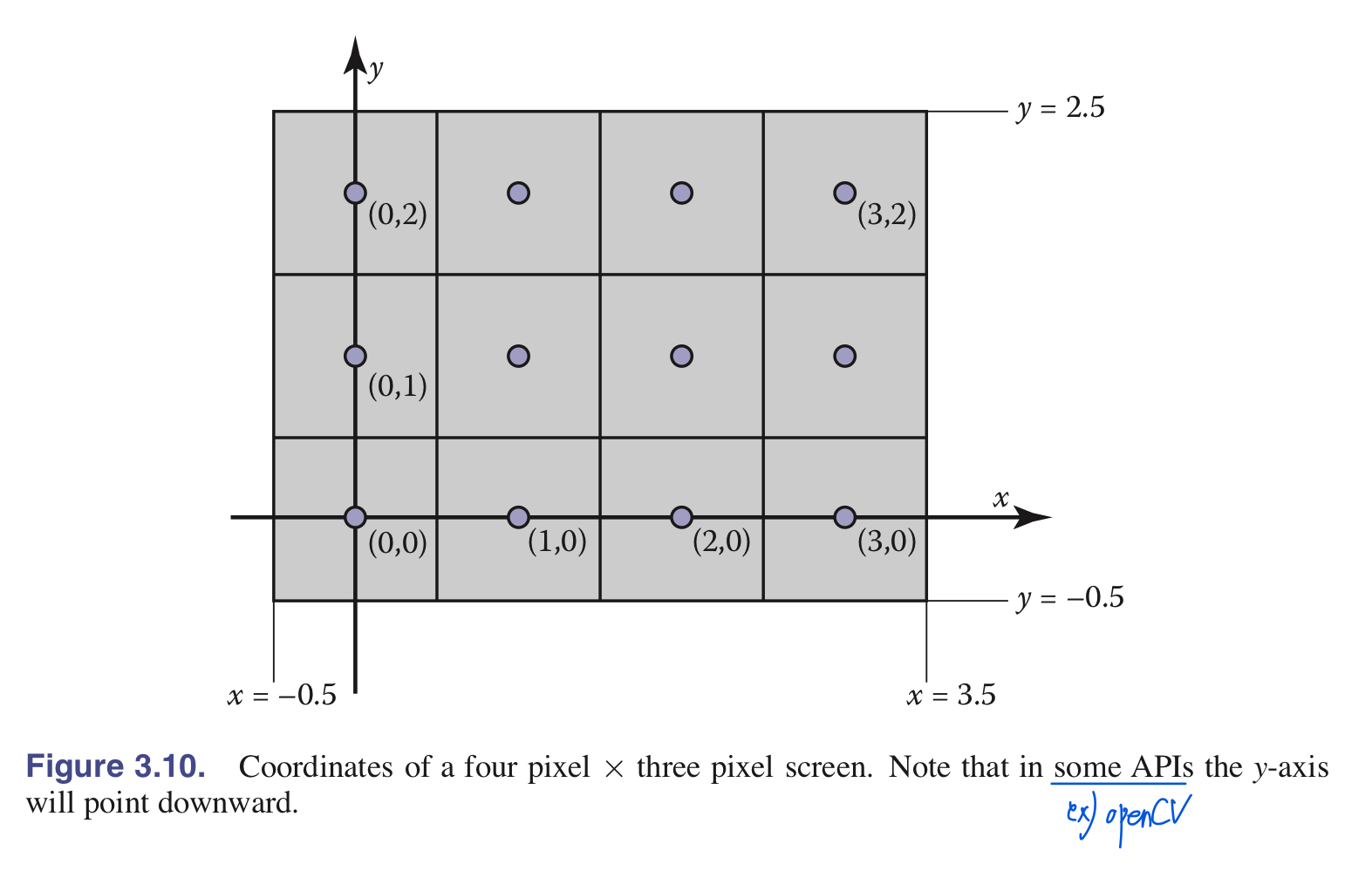
• 이미지 width가 $n_x$, 높이가 $n_y$일 떄, image rectangular domain은 다음과 같이 평행이동을 0.5씩 했다면 top-right pixel도 똑같이 평행이동시킨 만큼으로 설정할 수 있다; \(R = [-0.5, n_x - 0.5] \times [-0.5, n_y - 0.5]\)
  

2.1. Pixel Values

• Pixel formats :
  • 비트 수가 줄어들면, artifact나 flaws(결함)부분이 이미지상에 생길 수도 있다

2.2. Monitor Intensities and Gamma

• 모니터는 pixel “value”를 digital input으로 받아서, “intensity” level(빛의 강도)로 변환함
• 인간의 강도에 대한 인지는 비선형적이라서 이 단원에서 논할 부분은 아님(chapter 20에 나옴)
• 모니터도 input에 대해서 non-linear하게 처리하는데, 예를 들어 모니터에게 0, 0.5, 1.0의 세 픽셀 value를 주었을 때, 디스플레이되는 intensity는 0, 0.025, 1.0으로 처리됨

• 이러한 근사 비선형성은 $ \gamma $에 의해 결정됨
  \(displayed-intensity = (maximum-intensity) a^\gamma\)

• 이 때, a는 아래 그림의 체커보드 이미지를 통한 standard technique을 통해 찾을 수 있는 값임 (calibration과 연관된 건가?)

• “Gamma Correct”
  • gamma값을 알고 있으면, input을 감마 변형해서 $a = 0.5$ 즉, 흑백의 중간 강도에 대해 디스플레이되게 할 수 있음, 아래의 변형과정을 거친다
  • $a’ = a^{\frac{1}{\gamma}} $
  • \[: displayed-intensity = (a')^{\gamma} = (a^{\frac{1}{\gamma}})^{\gamma}(maximum-intensity) = a(maximum-intensity)\]

느낀점

• pixel 정의나 이미지에 대한 matching function같은 기초적인 개념을 훑고 가는 시작 단원이다,, 별 내용이 없음
• 설날인데 여유롭게 카공도 하고 기분이 좋다.ㅋㅋ