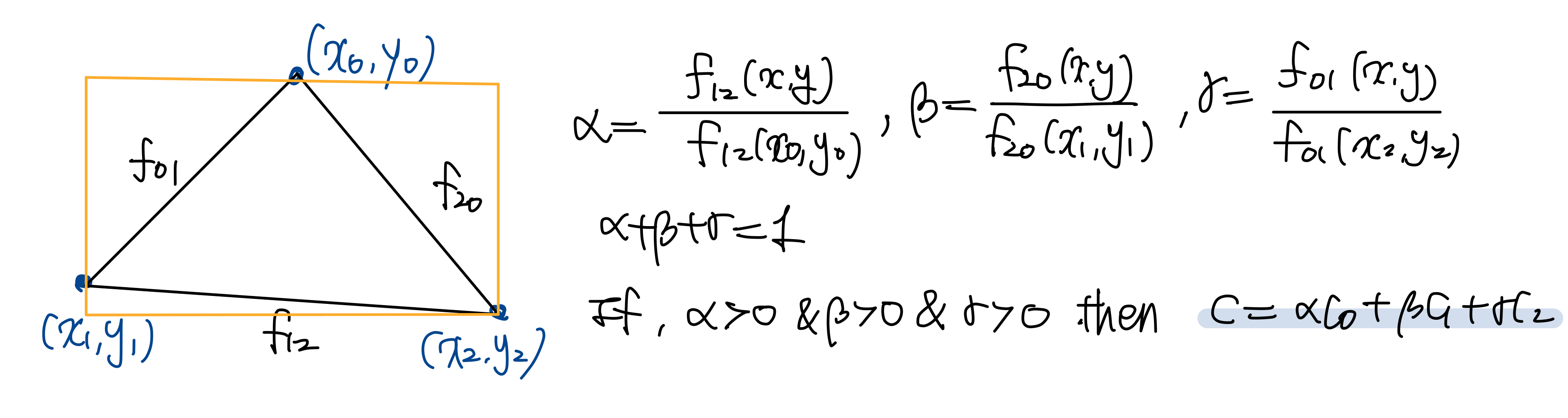Graphics-Ch8. Graphics Pipeline

Intro

• Graphics Pipeline : object에서 시작해서 pixel이 업데이트되기까지의 일련의 operations sequence
• object-order rendering = rendering by “rasterization”
• 그래픽스 파이프라인 과정들 중에서 “vertex processing”, “Rasterization”, “Fragment Processing”, “Blending” 이렇게 핵심 네 스텝에 대해서 이번 단원에 다루도록 하겠다
  • Vertex processing : vertices(꼭짓점)들이 연산되는 과정
  • Rasterziation stage : 그 꼭짓점들을 이용한 primitives가 보내져서 연산되고, 각각의 Primitive를 fragment로 쪼갬
  • Fragment processing : 쪼개진 fragment들이 연산되는 과정
  • Blending : 다양한 Fragment들이 대응되는 픽셀에 따라서 혼합됨

1. Rasterization

• 그래픽스 파이프라인 중 가장 핵심이 되는 과정
• rasterizer는 다음의 두 가지 일을 수행함
  1. 픽셀을 순회함, 각 픽셀은 primitive로 덮여있음
  2. 그 primitive들을 보간(Interpolate)함

1.1. Line Drawing

• 오든 그래픽스 패키지들은 line drawing관련된 명령을 포함하고 있음
• 시작점 $(x_0, y_0)$과 끝점 $(x_1, y_1)$을 연결하는 직선 그리기
• 크게 implicit line equation을 이용하는 방법과 parametric한 line equation을 이용하는 방법으로 2가지 방법이 있음

1.1.1. Implicit Line Equations

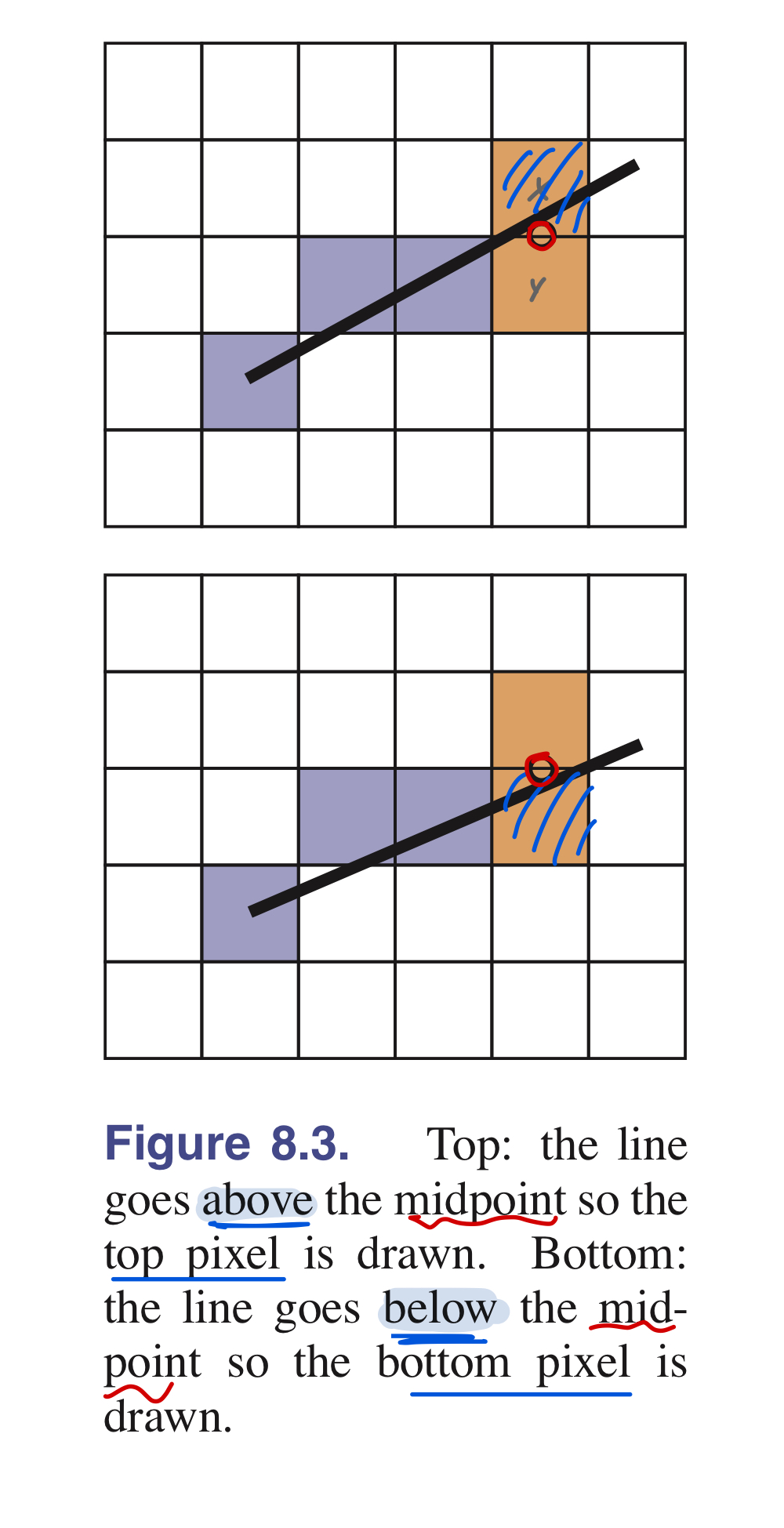
• Midpoint alogrithm 이용: 직선의 방정식 $f(x,y)$가 이 midpoint보다 위에 있는지 아래에 있는지에 따라서 픽셀 선택하는 알고리즘
• 시작점 끝점을 잇는 직선의 방정식 $f(x,y)$일 떄, 기울기 $m = \frac{y_1 - y_o}{x_1 - x_0}$
• 직선 위에 있는 점들에 대해서는 $f(x,y)=0$을 만족한다는 성질 이용
• $(x, y)$에서 다음으로 이동할 픽셀의 후보군(아래 그림에서 주황색 픽셀들)을 다음의 두 가지로 설정함 : $(x+1, y)$ 또는 $(x+1, y+1)$
  • 평행하게 오른쪽 한 칸으로 움직이거나, 대각선 방향으로 이동하는 경우의 수
• Midpoint = $(x+1, y+0.5)$

$f$가 midpoint보다 above한지, below한지 분류하는 방법 : $d = f(x+1, y+0.5)$라고 할 때, 1. if $d < 0$이라면 대각선 방향으로 즉, $(x+1, y+1)$ 으로 픽셀 결정 2. else $d > 0$이라면, 평행한 방향으로 즉, $(x+1)$ 으로 픽셀 결정

1.2. Triangle Rasterization

• 2D points로 2D 삼각형 그리는 방법
  • Given points $p_0 = (x_0, y_0)$ , $p_1 = (x_1, y_1)$, $p_2 = (x_2, y_2)$ in screen space
  • 각 꼭짓점이 color $c_0, c_1, c_2$를 저장하고 있다는 가정하에, 삼각형 위의 한 점을 $(\alpha, \beta, \gamma)$계수르 이용하여 표현 가능 ( barycentric 좌표계를 이용):
    
  \[\begin{align} c = \alpha c_0 + \beta c_1 + \gamma c_2. \end{align}\]
  • 위 방법의 interpolation을 “Gouraud interpolation“(고러드 보간, 고러드 쉐딩이랑 차이점 공부하기)이라고도 부름
• line drawing이랑 삼각형 rasterization의 미묘한 차이점중에 하나는 vertices and edges에 있다.
  1. “Hole problem”: 인접한 삼각형을 그릴 떄, hole이 생기면 안됨
  2. “Order problem” : 만약 인접한 삼각형들이 다른 색상을 갖고 있다면 그려지는 순서에 따라서 이미지 색상이 달라짐

이 두가지 문제를 완화하기 위해, 삼각형의 center가 삼각형 내부에 존재할때만 픽셀을 그리는 성질을 이용함 (당연한거 아님?)

• 같은 말로, barycentric coordinate상에서 삼각형의 중심점(center)이 (0,1)간격 사이에 존재해야 한다는 의미

• 만약, center가 삼각형의 edge에 정확하게 존재하면 어떻게 하는가?? 이 질문에 대한 내용은 후에 다룬다

• Barycentric Coordinate을 통해 삼각형같은 다면체의 “꼭짓점”이 주어지는 상황에서 어떤 위치의 픽셀에 그릴지와 그 픽셀의 색상또한 결정하는 key가 된다.
• 모든 픽셀에 대해서 고러드 보간을 이용하면 계산 복잡성이 크기 때문에, 아래의 간단한 방법으로 효율성 증가시킬 수 있음
  • 삼각형의 세 꼭짓점을 기준으로 한 bounding rectangle을 찾아서 이 직사각형 내부에 존재하는 후보 픽셀들에 대해서만 계산 Looping을 진행한다

알고리즘

x_min = floor(x_i)
x_max = ceiling(x_i)
y_min = floor(y_i)
y_max = ceiling(y_i)

for y in range(y_min, y_max + 1):
    for x in range(x_min, x_max + 1):
        α = f_12(x, y) / f_12(x_0, y_0)
        β = f_20(x, y) / f_20(x_1, y_1)
        γ = f_01(x, y) / f_01(x_2, y_2)

        if α > 0 and β > 0 and γ > 0:s
            c = α * c_0 + β * c_1 + γ * c_2
            drawpixel(x, y, color=c)

• 여기서 $f_{ij}$는 꼭짓점을 잇는 직선의 방정식(line drawing 섹션)이고 아래처럼 표현함 \(\begin{align} f_{01}(x,y) &= (y_0 - y_1)x + (x_1 - x_0)y + x_0y_1 - x_1y_0 , \\ f_{12}(x,y) &= (y_1 - y_2)x + (x_2 - x_1)y + x_1y_2 - x_2y_1 , \\ f_{20}(x,y) &= (y_2 - y_0)x + (x_0 - x_2)y + x_2y_0 - x_0y_2 . \end{align}\)

  

Dealing with Pixels on Triangle Edges

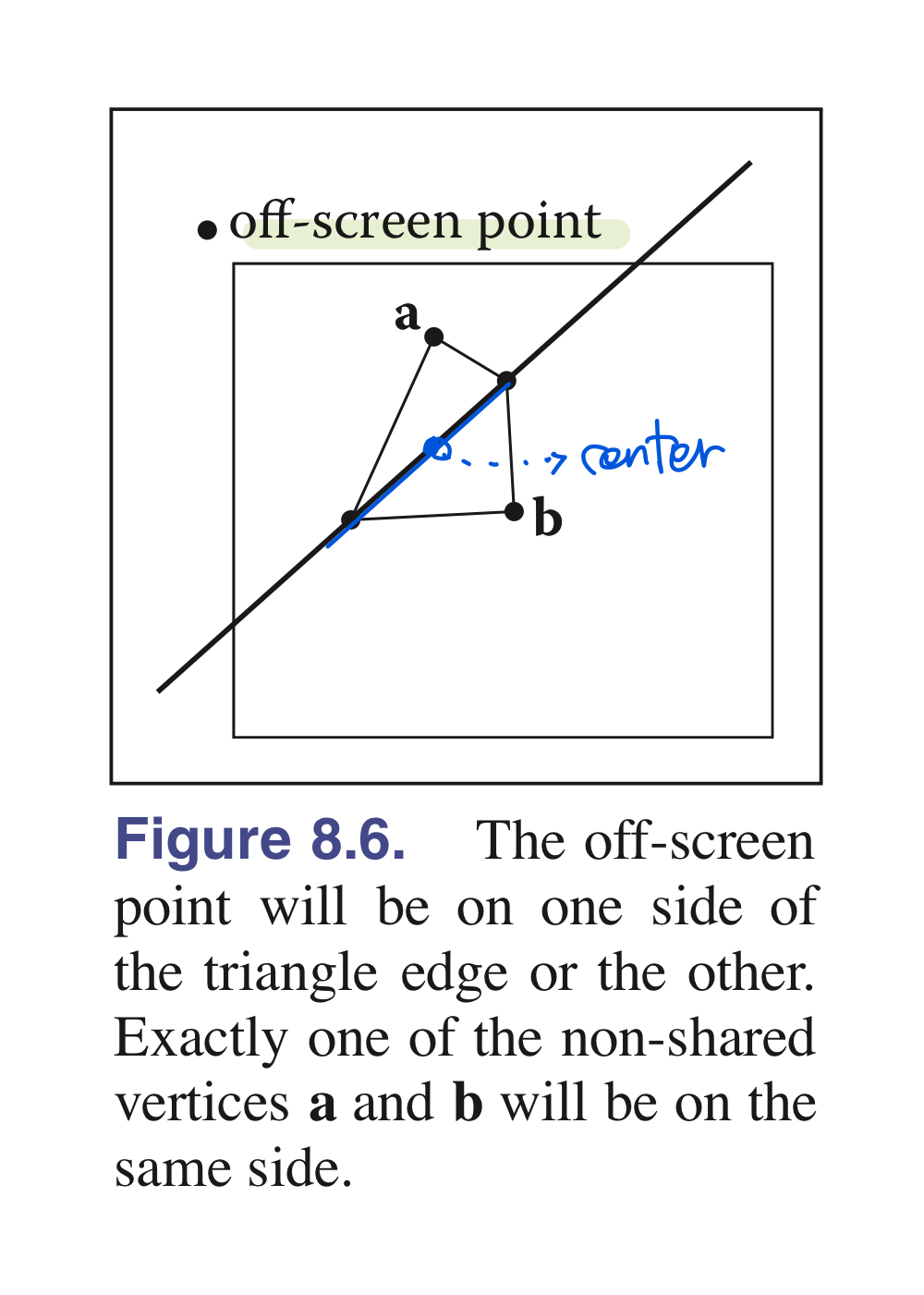
• 삼각형의 중심(center)이 Edge에 정확하게 존재하는 경우의 픽셀은 어떻게 결정할 것인지에 대한 내용
• 삼각형 중심이 삼각형 변에 위치하는 대표적인 예시가 직각-삼각형임

"off-screen point"는 두 삼각형의 공유된 변의 정확히 한쪽에 위치하며, 우리가 그릴 edge는 바로 그 변임, 공유 변 위에 있지 않은 정점들은 해당 변 기준으로 서로 반대쪽에 위치한다.

• 따라서, 그림 상 a 또는 b 정점 중 하나는 off-screen point와 shared edge기준 같은 부호면을 가진다는 성질이용
• $pq > 0$

알고리즘

y_max = ceiling(y_i)

f_α = f_12(x_0, y_0)
f_β = f_20(x_1, y_1)
f_γ = f_01(x_2, y_2)

for y in range(y_min, y_max + 1):
    for x in range(x_min, x_max + 1):
        α = f_12(x, y) / f_α
        β = f_20(x, y) / f_β
        γ = f_01(x, y) / f_γ

        if α >= 0 and β >= 0 and γ >= 0:
            if (α > 0 or f_α * f_12(-1, -1) > 0) and \  # 부호
               (β > 0 or f_β * f_20(-1, -1) > 0) and \  # 부호
               (γ > 0 or f_γ * f_01(-1, -1) > 0):       # 부호

                c = α * c_0 + β * c_1 + γ * c_2
                drawpixel(x, y, color=c)

1.3. CLipping

• 눈의 뒤(behind)에 존재하는 공간 혹은 view volume의 바깥에 존재하는 primitive를 clipping해주는 과정들이 있어야 정확한 Rasterizing을 수행할 수 있다.
• 삼각형에서 두 정점은 view volume 내부에 존재하지만, 하나의 정점이 behind the eye에 있다는 상황을 생각해보자.
  • perspective transformation을 하게 되면, depth $z$가 $z’$로 변환되고 부호도 반대로 바뀜
  • 이떄 모든 정점이 view volume에 있지 않는다면 제대로 transformation이 이루어지지 않아서 삼각형 모양도 변형되는 incorrect result가 초래됨
• Clipping : removes part of primitives that could extend behind the eye (시야에 보이지 않는 primitives들을 제거하는 역할)
  

1. transform되기 이전 단계의 6개의 평면을 이용하여 표현된 world coordinate들에서 수행되는 clipping module
2. homogeneous coordinate을 이용하여 4D transform된 space에서 수행되는 clipping module
   • 위의 두 가지 옵션을 통해 clipping 작업이 수행된다.

1.4. Clipping against a Plane

• 평면의 방정식 : $f(\mathrm{p}) = \mathrm{n} \cdot (\mathrm{p}-\mathrm{q}) = 0$ 이 implicit equation을 다시 쓰면 아래처럼 재표현 가능:

  \[\begin{align} f(\mathrm{p}) = \mathrm{n} \cdot \mathrm{p} + D = 0, \end{align}\]
• points $a$와 $b$를 잇는 line segment가 있는 상황에서, 이 선분은 평면에 의해 clipping되어짐
• 평면 $f(\mathrm{p}) > 0$ 이면 평면의 내부(inside)에 존재하는 것이고, $f(\mathrm{p}) < 0$이면 평면의 외부(outside)에 존재하는 것임
  • clipping된 선분의 양끝 지점에 대한 부호가 다르다는 성질
• 선분과 평면이 만나는 intersection point $\mathrm{p}$ ($\mathrm{p} = a + t(b-a)$)에서의 $f(\mathrm{p}) = 0$이라는 성질 이용해서 아래 그림처럼 교차점에서의 $t$값을 도출할 수 있다.

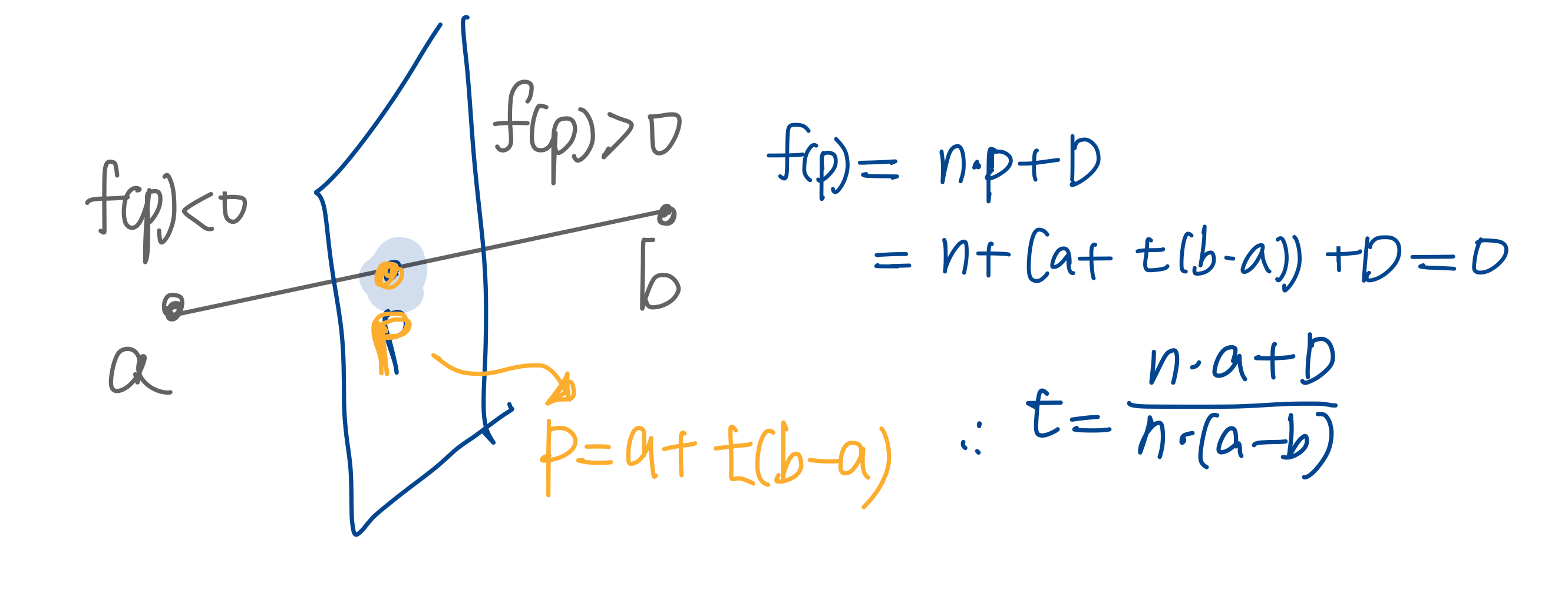
2. Operations Before and After Rasterization

• Graphics pipeline을 recall
  • Rasterization 이전에 “Vertex processing” 단계를 통해 geometry들이 적절하게 transformed되어 primitives로 도출되어야 함
    • 이 때, viewing transformations을 이용해서 world coordinate에서 screen space로 변환되는 정보들 + colors, surface normals, texture coordinate 같은 정보들도 변환되어야함
    • 전자는 chapter 7에서 다루었기 때문에 후자의 내용을 이번 챕터에서 어떻게 변환시키는지 다루도록 한다.
  • Rasterization 이후에는 “Fragment processing” 단계를 통해 rasterization으로 나온 interpolated color와 depth를 그대로 통과시키던가,아니면 복잡한 shading operation으로 각각의 fragment에 대한 color와 depth를 계산한다.
  • 그 후, “Blending” 단계를 통해 각 픽셀마다 겹쳐있는 primitive에서 final color를 혼합시켜 결정한다.
    • 가장 쉽고 흔한 방법으로는 depth가 가장 작은, 즉 eye와 가장 가까운 fragment의 color로 선택하는 것
      

2.1. Simple 2D Drawing

• 가장 간단한 파이프라인은, vertex와 fragments stage, 그리고 blending stage 에서 아무것도 수행되지 않고 오로지 rasterization에서 pixel coordinate에 직접적으로 연산들이 모두 수행되는 것
  

2.2. A Minimal 3D Pipeline

• 3D 공간에 물체를 그리기 위해서는 2D Drawing pipeline에서 matrix transformation이 포함되어 vertex processing이 이루어진다.
  • vertex-processing에서 인풋으로 들어오는 vertex position에다가 camera, projection, 그리고 viewport transformation같은 행렬을 곱함으로써 행렬 변환이 수행됨

• 이 결과로 삼각형이 screen space에 띄워질 수 있고, 이것은 2D상에 직접적으로 그려지는 것과 같은 결과임

• Occlusion problem : back-to-front 순서로 물체들을 그리지 않으면, 더 가까이 있는 물체가 멀리 있는 물체에 가려지는 incorrect result가 초래됨
  • 이 back-to-front 순서로 물체 그리는 걸 Painter’s algorithm이라고도 부름
  • hidden surface를 제거하는 가장 타당한 방법임
  • 하지만, Occlusion cycle같은 어떤 물체가 더 앞에 있고 뒤에있는지 이 상대적인 깊이를 평가할 수 없는 경우가 존재함
    • 이럴때는 painter’s algorithm으로 back-to-front order를 설정할 수가 없다.
    • 또한, depth 기준으로 primitives를 정렬하는 것은 시간소요적이라서 큰 씬에 대해서는 애초에 painter’s algorithm을 사용하기가 거의 어려움
      

2.3. Using a Z-Buffer for Hidden Surfaces

• 앞선 occlusion problem에서 필요한 depth sorting이 시간소요적이라는 측면에서, painter’s algorithm이 거의 사용되지 않기 떄문에 나온 방법
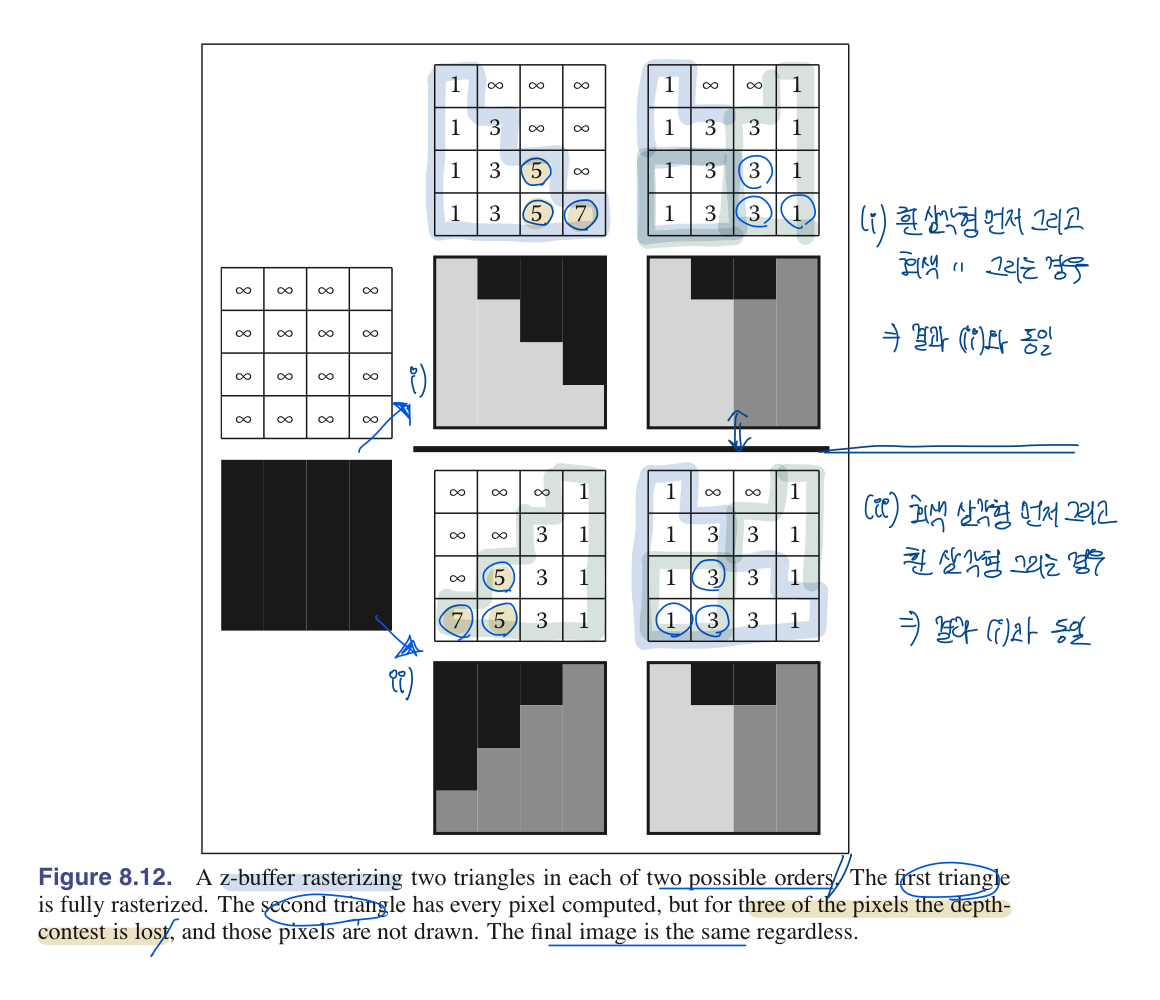
• 아이디어 = 각 픽셀에서 지금까지 렌더링된 가장 가까운 표면까지의 거리(depth)를 기록하고, 그 거리보다 더 멀리 있는 fragment는 폐기한다.
  • 이 거리를 RGB color 세 값에 추가적으로 buffer를 두어 z값을 저장하고 z차원에서 grid를 생성함
• buffer algorithm은 Fragment blending phase에서 구현됨
• 현재 z-buffer에 저장된 depth value랑 각 fragment별로 depth를 비교하면서, 만약 해당 fragment value값이 더 작다면 color와 depth value를 덮어씌운다.
  

2.4. Per-vertex Shading

• rasterization으로 interpolated된 color와 계산된 depth로만 3D 공간에서 object를 나타내는 것으로 충분할 수도 있지만, 대부분은 objects with shading을 구현하고 싶어함
• light direction, eye direction, surface normal 같은 조명과 관련한 변수들 필요로 함
• vertex stage에서 shading computation을 수행하는 방법 소개
  • “고러드 쉐이딩”
  • 카메라 poistion, lights, vertex에 의해서 빛의 방향과 viewer의 gaze direction이 계산되는 방법
  • 이 shading equation을 통해 계산된 vertex color는 rasterizer에게 넘어감 (즉, rasterizer 이전 단계에서 수행되는 shading equation이다)
• 각각의 vertex에서 shading을 다루고 vertex끼리는 다루지 않아서 아무래도 디테일이 좀 떨어진다는 단점이 있다.
  

2.5. Per-fragment Shading

• Rasterization 이후에 나온 interpolated color를 이용해서 fragment stage에서 수행되는 shading
• “Phong shading” (Phong illumination model이랑 다른 개념임)
• shading equation자체는 똑같지만, 정점 각각에 행해지는 것이 아니라 rasterziation으로 나온 보간된 색상을 이용한 fragment각각에 수행된다는 점이 다름
  • 이것을 위해서 vertex stage 좌표계가 fragment stage와 일련되게 존재해야 데이터가 적절하게 사용될 수 있음
    

2.6. Texture Mapping

• Texture에 대한 디테일은 chapter-11에서 더 자세하게 다룰 예정
• Textures : 표면의 음영(shading)에 추가적인 디테일을 더하기 위해 사용되는 이미지로, 추가되지 않으면 지나치게 균일하고 인공적으로 보이게 될 수 있음
  

2.7. Shading Frequency

• shading computation들을 어떤 스텝에 위치시킬지를 color change가 얼마나 빠른지에 따라 결정할 수 있다.
• 이 변하는 정도를 “scale”로 확인할 수 있음
  1. large-scale features(e.g., diffuse shading(난반사된 빛) on curved surfaces)
     • low shading frequency로 계산되어야 함
     • vertex stage
  2. small-scale features(e.g., sharp highlightsor detailed textures)
     • high shading frequency로 계산됨
     • vertex stage & fragment stage 모두 가능

---

simple anti-aliasing, culling primitives 내용 교재 참고