Graphics-Ch9. Signal Processing
Graphics-Ch9. Signal Processing
Intro
- 신호 처리 단원
- Sampling(연속적인 아날로그 신호에서 이산적인 디지털 신호로 샘플링하는 과정)과 Reconstruction(이산적인 신호 -> 연속적인 아날로그 신호)의 일련의 과정에서 수행되는 filtering, anti-aliasing, Fourier transform,등의 내용을 다룸
- 학부 패턴인식 수업 중간범위에서 배웠던 내용이랑 많이 겹침, 나중에 참고
1. Digital Audio : Sampling in 1D
- Continuous Analog signal $\rightarrow$ Lowpass filter $\rightarrow$ ADC(A/D converter : Sampling) $\rightarrow$ Discrete digital signal
- Discrete digital signal $\rightarrow$ DAC(D/A converter : Reconstruction) $\rightarrow$ Lowpass filter $\rightarrow$ Continuous analog signal
- Undersampling : 너무 적은 sample rate으로 샘플링하면(듬성듬성) ambiguous result를 초래하기 때문에, artifact가 생길 수 있음
1.1. Sampling Artifacts and Aliasing
- undersampling으로 생긴 artifact를 완화하는 방법은?
- sampling이전에 filtering을 해주고, reconstruction이후에 filtering을 수행하기
- undersampling으로 생긴 artifact를 완화하는 방법은?
- Aliasing : sampling 이후 결과만 보면 원본 아날로그 신호가 빠른 sine wave였는지, 느린 sine wave였는지 원본을 알 수 없다
- 이런 두 경우에, reconstruction을 적절하게 수행할 간단한 방법을 찾기가 쉽지않음
- 이때 high-frequency signal이 low-frequency signal “처럼 되려고 하는” 현상을 aliasing이라고 함
- sampling과 reconstruction과정에서 다루어지는 challenges :
- Sample rate을 얼마나 키워야 적절할까
- 어떤 종류의 Filter를 사용해야하는가
- smoothing의 정도($\alpha$)를 어느정도로 해야하는가
2. Convolution
- 합성곱 연산 내용
- $f(x), g(x)$ : continuous function
- $a[i]$ : discrete function
- $f \star g$ : $f$와 $g$의 convolution 연산, $f$를 $g$로 convolved했다고도 표현함
2.1. Moving Averages (이동평균)
- 각 포인트에 대해 일정 범위(radius $=r$)안에서 평균치를 계산하는 것은 얼마나 smoothing시킬것인지에 대한 연산으로 생각할 수 있음
continuous function $g(x)$에 대한 이동평균 값 :
\[\begin{align} h(x) = \frac{1}{2r} \int_{x-r}^{x+r} g(t) \,dt \end{align}\]discrete function $a[i]$에 대한 이동평균 값 :
\[\begin{align} c[i] = \frac{1}{2r+1} \sum_{j=i-r}^{j=i+r} a[j] \end{align}\]
2.2. Discrete Convolution
sequence $a$를 filter $b$로 convolution :
\[\begin{align} (a \star b)[i] &= \sum_{j}a[j]b[i-j] \\ &= \sum_{j=i-r}^{i+r} a[j]b[i-j] \end{align}\]- $b[i-j]$ : position $j$에서의 샘플에 대한 가중치 역할
- convolution연산에는 교환(commutative)법칙, 결합(associative)법칙, 분배(distributive)법칙 모두 성립
- $d$ : discrete impulse $\rightarrow$ 한 point에서만 1 신호를 갖고 나머지는 모두 0
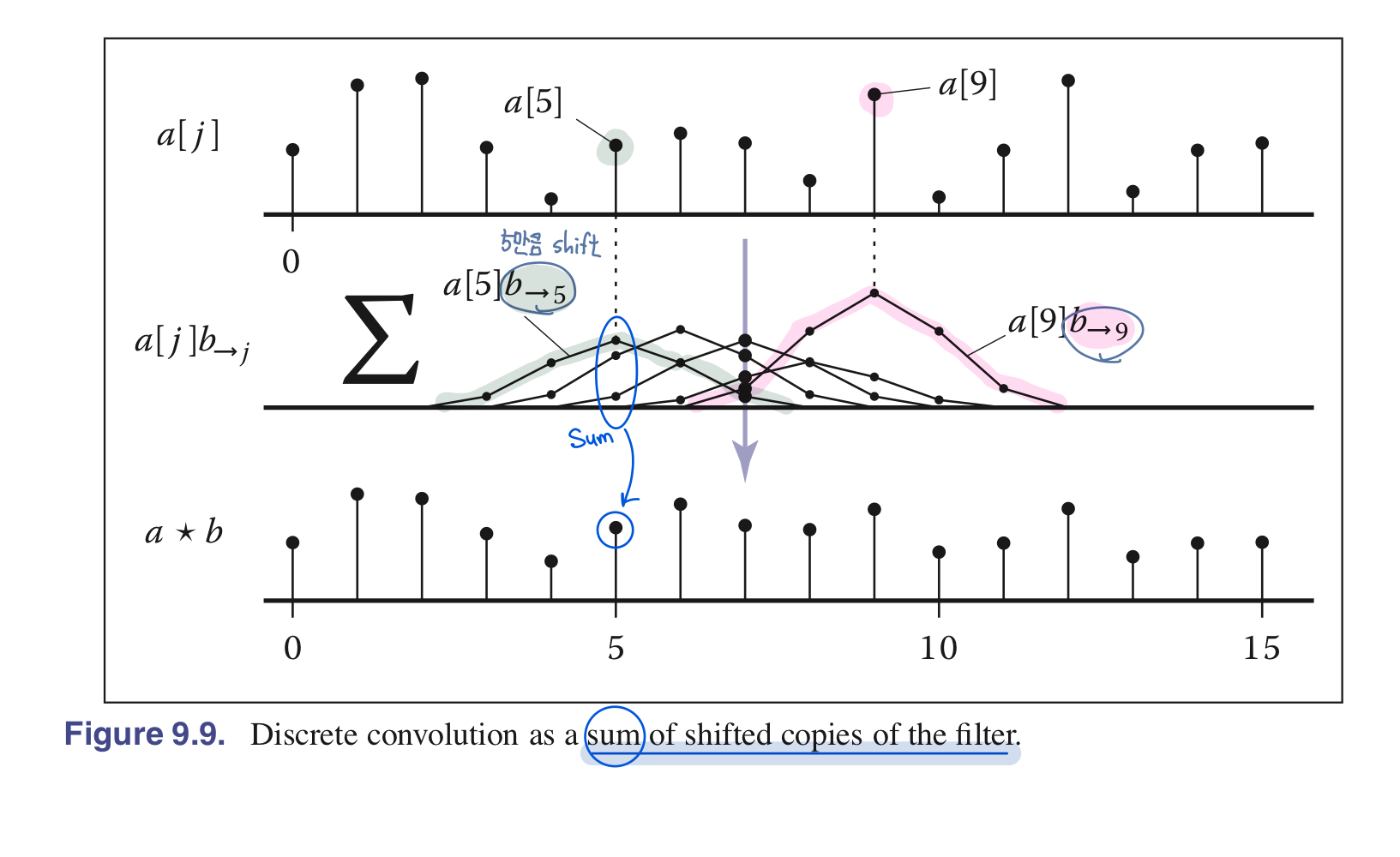
2.3. Convolution as a Sum of Shifted Filters
\[\begin{align} b_{\rightarrow j}[i] = b[i-j] \end{align}\] \[\begin{align} (a \star b)[i] &= \sum_{j}a[j]b_{\rightarrow j}[i] \end{align}\]2.4. Convolusion with Continuous Functions
- 두 연속함수에 대한 convolution 연산을 아래와 같이 표현할 수 있음 :
\(\begin{align} (f \star g)(x) = \int_{-\infty}^{+\infty} f(t) g_{\rightarrow t} \,dt. \end{align}\) 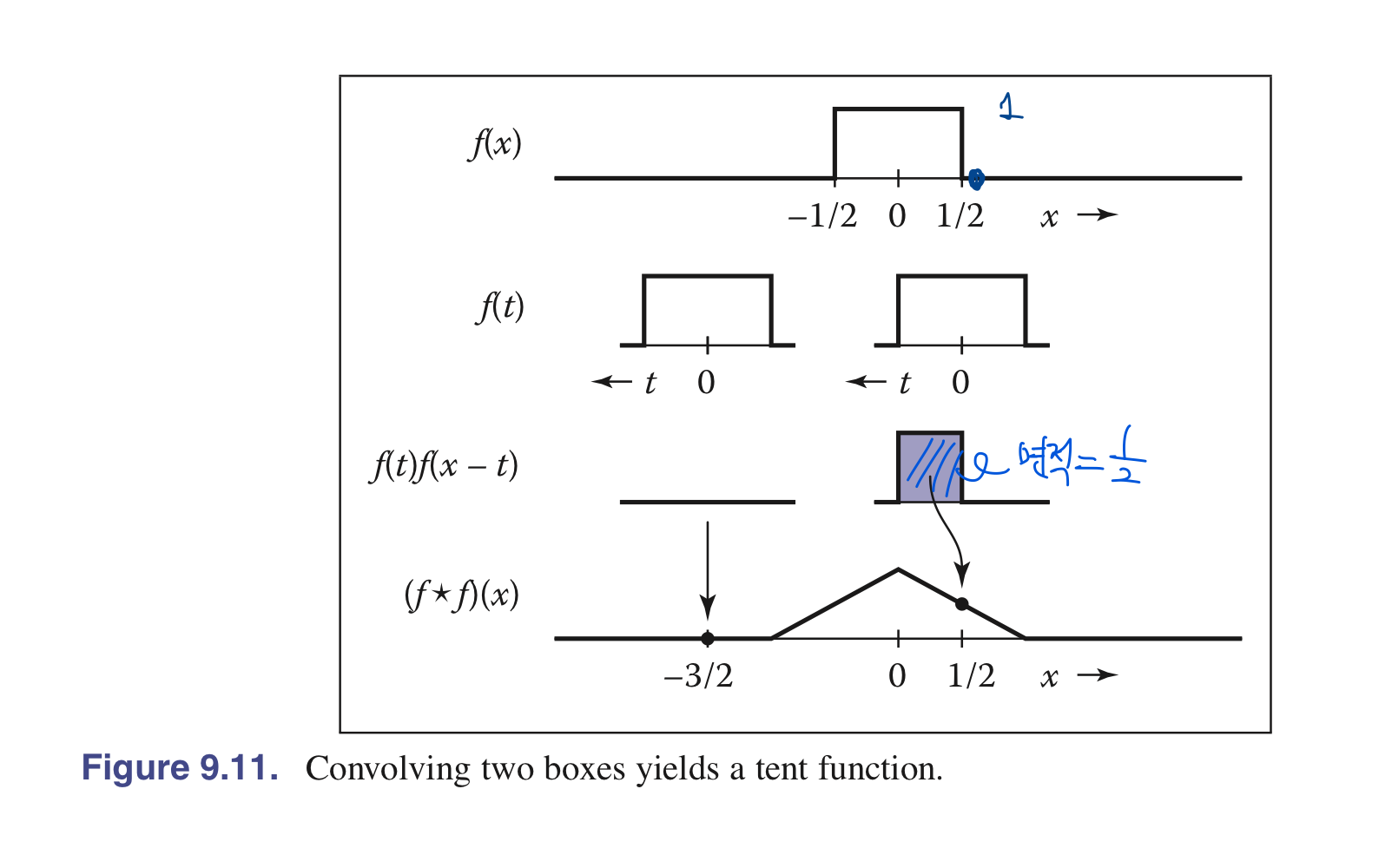
Dirac Delta Function $\delta(x)$
- delta function $\delta(x)$ : x = 0일때만 impulse 1값을 갖는 continuous identity function
- 이므로, discrete impulse $d \star a = a$이런 성질처럼 delta function에서도 $\delta \star f = f$ 수식이 성립함
2.5. 2D discrete convolution
- 1차원보다 많아지는 컨볼루션 연산식은 어떻게 표현하는가, 똑같다. 차원만 늘리면 된다
3. Convolution Filters
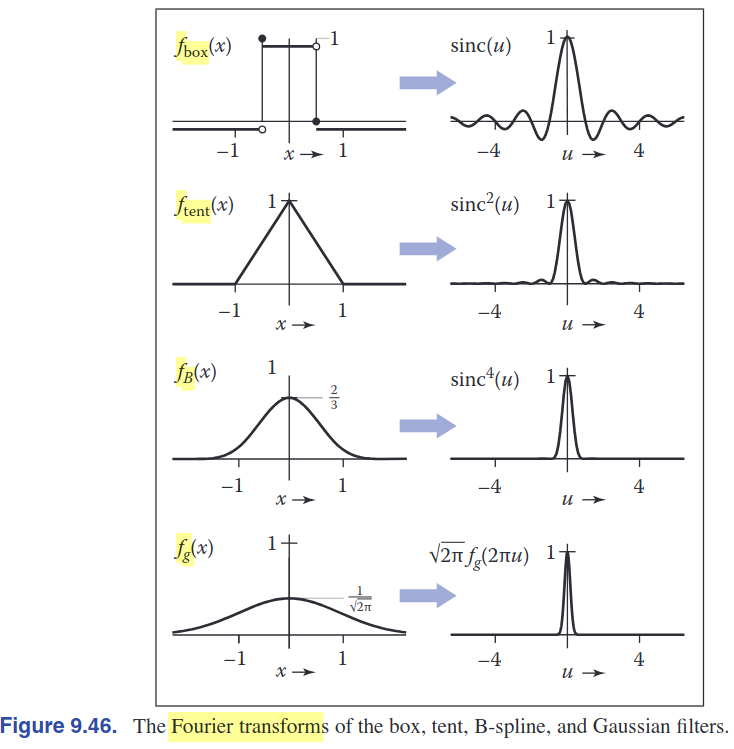
3.1. Box filter
\[\begin{align} a_{\text{box},r}[i] &= \begin{cases} \frac{1}{2r+1}, & \text{if } |i| \leq r \\ 0, & \text{otherwise} \end{cases} \\ f_{\text{box},r}(x) &= \begin{cases} \frac{1}{2r}, & \text{if } -r \leq x < r \\ 0, & \text{otherwise} \end{cases} \end{align}\]3.2. Tent filter
\[\begin{align} f_{\text{tent}}(x) = \begin{cases} 1 - |x|, & |x| < 1, \\ 0, & \text{otherwise}.\end{cases} \end{align}\]3.3. Gaussian filter
\[\begin{align} f_{g, \sigma}(x) = \frac{1}{2\pi\sigma^2} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right) \end{align}\]- 표준편차 $\sigma$는 필터에서 얼마나 스무딩할것인지 강도를 조정할 수 있음
- 참고로 가우시안 분포에서 일정 band만큼 trimming(잘라내기)할수도 있는데, 이것을 trimmed Gaussian이라고 하며, 이때 trimmed Gaussian에서 스케일 $s$배만큼 늘리면 기존 가우시안분포로 복원시킬 수 있다는 성질 존재함
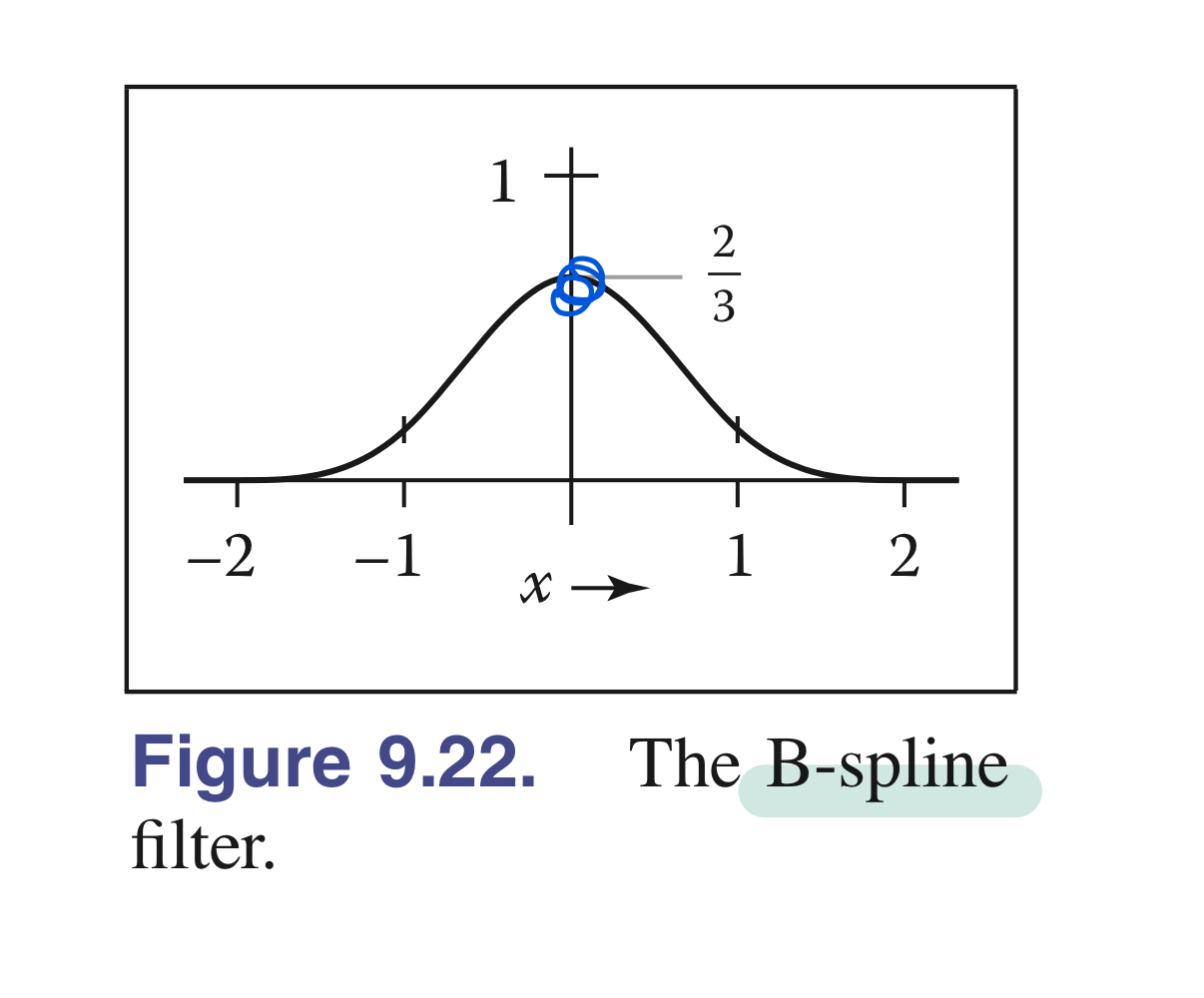
3.4. B-Spline Cubic filter
- 부드러운 보간을 제공하며, 부드러운 블러 효과를 줄 때 사용됨
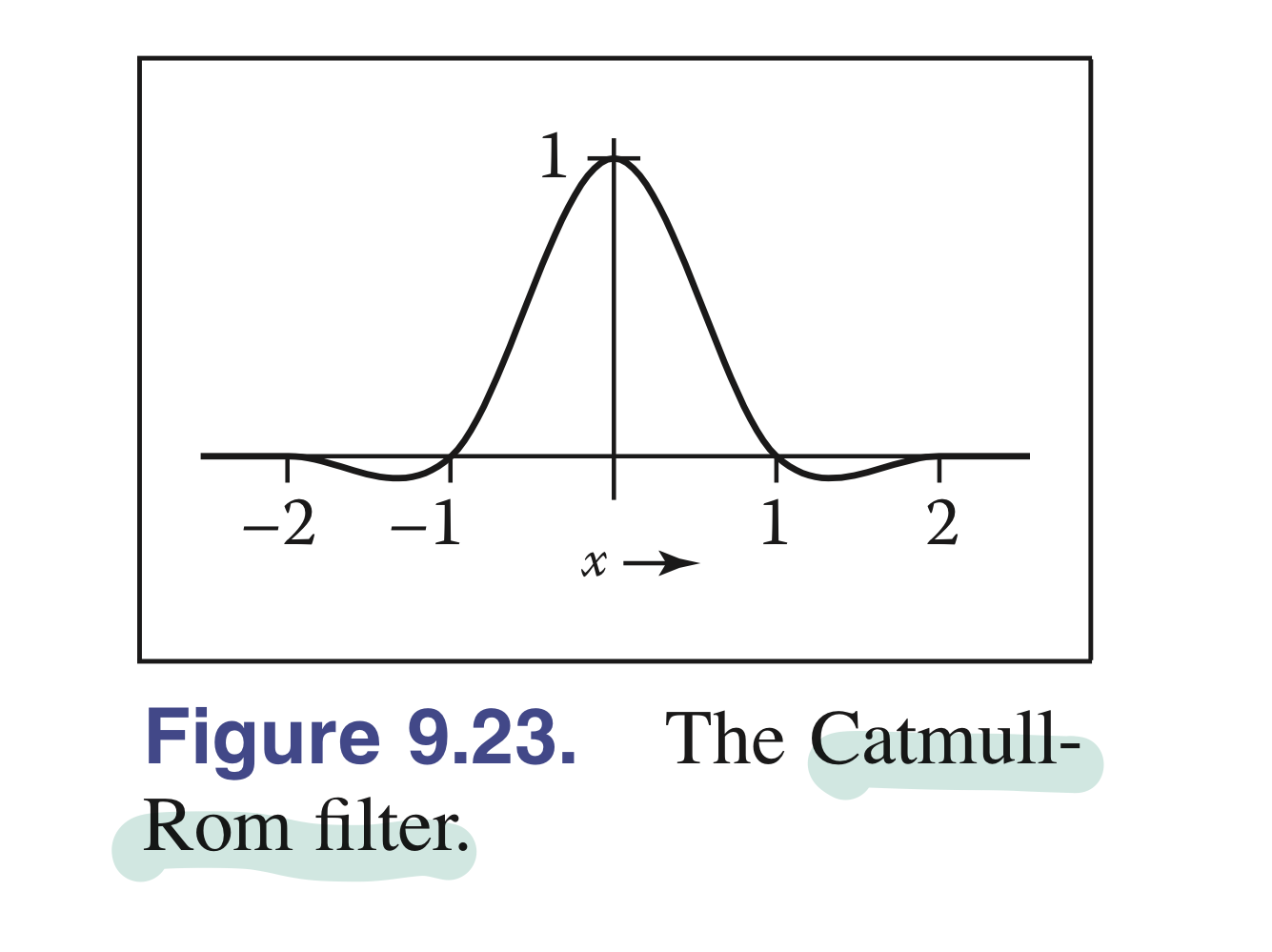
3.5. Catmull-Rom Cubic filter
- 날카로운 디테일을 유지하면서 부드러운 전환을 제공하는 특징
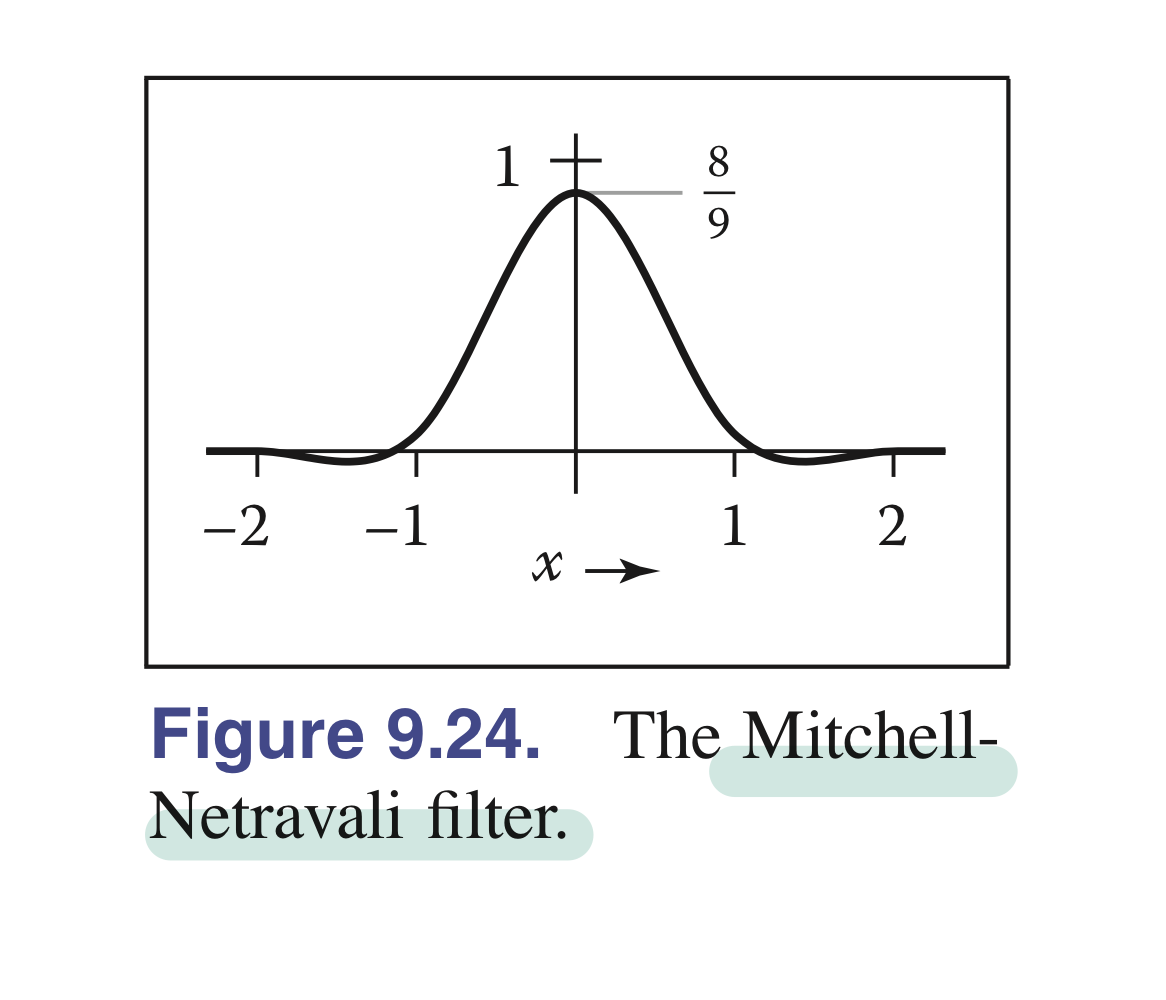
3.6. Mitchell-Netravali Cubic filter
- 두 개의 파라미터 B와 C를 조절하여 샤프니스와 스무딩을 균형 잡을 수 있음
Overshooting(Ringing)
- catmull-rom filter라던지, mitchell-netravali filter는 1과 2사이 그리고 -2와 -1사이에 필터 value가 0보다 작아지는 지점들이 존재함
이런 범위 부근에서 overshooting이라는 아래 그림처럼 extra oscillations(진동)이 초래되는 결과를 overshoot되었다고 함
4. Signal Processing for Images
- 블러링은 그냥 위 그림처럼 box filter, gaussian filter처럼 low pass filter를 기존 이미지에 convolution 연산해주면 구현됨
“Sharpening”
식 유도과정 :
\[\begin{align} I_{\text{blur}} &= I \ast f_{g, \sigma} \\ I_{\text{sharp}} &= I + \alpha (I - I_{\text{blur}}) \\ &= I + \alpha (I - I \ast f_{g, \sigma}) \\ &= (1 + \alpha) I - \alpha (I \ast f_{g, \sigma}) \\ &= I \ast \left( (1+\alpha) \delta - \alpha f_{g, \sigma} \right) \\ &= I \ast f_{\text{sharp}} \end{align}\]
5. Sampling Theory
- 푸리에 신호와 관련된 샘플링 이론 관련한 내용
- 나이퀘스트 샘플링 이론이라던지 anti-aliasing 부분을 주파수 도메인의 푸리에 변환, 역푸리에변환과 관련되어 깊은 수학적인 내용을 다룸
5.1. Fourier Transform
- 푸리에 신호 내용
- Fourier Series
- 주기 $T$를 갖는 주기 신호 $x(t) = x(t+T)$가 존재할 때, fundamental frequency $w_0 = 2\pi / T$ 이다
- 이를 오일러 공식을 이용해서 cosine함수로 아래처럼 표현가능 :
\(\begin{align} x(t) = cos w_0 t \quad x(t) = e^{jw_0t} \end{align}\)\
Harmonically related complex exponentials 세트란?
\(\begin{align} \Theta_k(t) = e^{jkw_0t} = e^jk(2\pi /T)t \quad k = 0, +-1. +- 2, .. \end{align}\)- 이 때, 위의 harmonically related complex exponential들의 선형결합을 “Fourier Series Representation“이라고 함
- 그럼 주기가 없는(aperiodic)한 신호들에 대해서는 푸리에 변환으로 표현할 수 있다, sum말고 integral을 사용함
\(\begin{align} \hat{f(u)} &= \int_{-\infty}^{+\infty} f(x) e^{-2\pi i u x} \,dx \\ f(x) & = \int_{-\infty}^{+\infty} \hat{f(u)}e^{2\pi i u x} \,du \\ \int (f(x))^2 \,dx &= \int (\hat{f(u)})^2 \,du \end{align}\)
- 차례대로 Fourier transform을 이용해서 푸리에 계수(Fourier Coefficient)구하는 공식, Inverse Fourier Transform으로 원본 aperiodic signal을 표현하는 공식
…
5.4. Sampling and Aliasing
- 앨리아싱 현상을 완화하려면, 적절한 sampling filter와 reconstruction filter를 설정하는 것이 중요하다
- 이때 low pass filter로 filtering을 하는 목적은, 일정 주파수 도메인 범위를 잘라내서 제한하는 것임 $\rightarrow$ alias spectra 가 원본 신호를 방해하지 않게 도와줌
- “Nyquist Criterion“(나이퀘스트 샘플링 이론):
- 연속 신호를 디지털 신호로 변환(샘플링)할 때, 신호의 최대 주파수(f_{max})의 최소 두 배 이상으로 샘플링해야 정보 손실 없이 복원 가능
- 샘플링 실행하는 min frequency = 나이퀘스트 속도(Nyquist Rate) = 2f_{max}
This post is licensed under CC BY 4.0 by the author.